Kleene星號

Kleene 星號，或稱 Kleene 閉包，德語稱 Kleensche Hülle，在數學上是一種適用於字元串或符號及字元的集合的一元運算。當 Kleene 星號被套用在一個集合 時，寫法是 。它被廣泛用於正則表達式。

基本介紹

• 中文名：Kleene星號
• 外文名：Kleensche Hülle
• 或稱： Kleene 閉包
• 用於：正則表達式

定義及標記方法

給定集合V 設：

• V₀ = {ε} 即只包含空串
  
• V₁ = V
  

遞歸的定義集合V_{i+1 ，}這裡的

• V_i+1 = { wv: w ∈ V_i and v ∈ V } .
  

所以在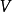 上的 Kleene 星號的定義是

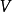
就是說，它是由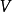 中的符號生成的所有可能的有限長度的字元串所構成的集合。

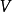
推廣

Kleene 星號經常推廣到任何么半群 ，也就是，一個集合 和在 上的二元運算 符合

(封閉性)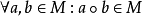

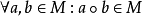
(結合律)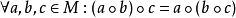

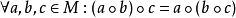
(單位元)

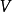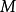如果 是 的子集，則 被定義為包含 (空字元串) 並閉合於這個運算下的 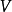的最小超集。接著 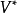自身是么半群，並被稱為 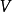生成的自由么半群。這是上面討論的 Kleene 星號的推廣，因為在某個符號的集合上所有字元串的集合形成了一個么半群(帶有字元串串接作為二元運算)。

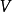
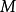
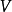
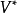
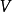
例子

Kleene 星號套用於字元串集合的例子：

• {"ab", "c"}* = {ε, "ab", "c", "abab", "abc", "cab", "cc", "ababab", "ababc", "abcab", "abcc", "cabab", "cabc", "ccab", "ccc", ...}
  

Kleene 星號套用於字元集合的例子：

• {'a', 'b', 'c'}* = {ε, "a", "b", "c", "aa", "ab", "ac", "ba", "bb", "bc", ...}
  

參考文獻

Kleene 星號的定義基本上可從任何一本自動機理論的參考書中找到。以下是其中一本標準的參考書：

• John Hopcroft | John E. Hopcroft and Jeffrey D. Ullman. Introduction to Automata Theory Languages and Computation. 1st edition. Addison-Wesley Publishing Company, 1979.