自動機理論是一種將離散數學系統的構造,作用和關係作為研究對象的數學理論。
在理論計算機科學中,自動機理論是對抽象機和它們能解決的問題的研究。自動機理論密切關聯於形式語言理論,因為自動機經常按它們所能識別的形式語言類來分類。
基本介紹
- 中文名:自動機理論
- 外文名:automata theory
- 領域:數學理論
- 關聯:形式語言理論
簡介
術語
詳細內容
 自動機理論
自動機理論
自動機理論是一種將離散數學系統的構造,作用和關係作為研究對象的數學理論。
在理論計算機科學中,自動機理論是對抽象機和它們能解決的問題的研究。自動機理論密切關聯於形式語言理論,因為自動機經常按它們所能識別的形式語言類來分類。
 自動機理論
自動機理論自動機理論是一種將離散數學系統的構造,作用和關係作為研究對象的數學理論。在理論計算機科學中,自動機理論是對抽象機和它們能解決的問題的研究。自動機理論密切關聯...
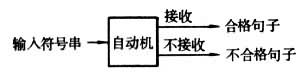
抽象自動機是—種能夠識別語言的抽象裝置,它不是具有物理實體的機器,而是表示計算機運算方式的抽象的邏輯關係系統,這樣的抽象自動機可以用來檢驗輸入的符號串是不是...
《形式語言與自動機理論》是2007年由機械工業出版的書籍,作者是吳哲輝。...... 《形式語言與自動機理論》是2007年由機械工業出版的書籍,作者是吳哲輝。...
形式語言與自動機理論是計算機科學與技術專業的一門重要課程。本書是作者結合其近30年來在大學講授該門課程的經驗和體會,選擇和組織有關內容撰寫而成。基於計算機...
有限自動機(finite automata)亦稱時序機,有限離散數字系統的抽象數學模型。一個有限自動機M由五元組(X,Y,S,δ,λ)給定,其中X,Y和S都是非空有限集,分別稱為M...
自動機理論、語言和計算導論 第2版)John E.Hopcroft,Rajeev Motwani,Jeffrey D.Ullman 編著本書是一本有關自動機理論、形式語言和計算機理論的經典著作。第1版...
《自動機理論.語言和計算機導論》(英文版)(第3版)是關於形式語言、自動機理論和計算複雜性方面的經典教材,是三位理論計算大師的巔峰之作,現已更新到第3版。書...
《自動機理論、語言和計算導論》是2008年機械工業出版社出版的圖書,作者是霍普克羅夫特 (John E.Hopcroft)。...
《自動機理論與套用》是2009年清華大學出版社出版的圖書,作者是里奇。...... 《自動機理論與套用(影印版)》闡述了計算科學的優美理論基礎,通過演示計算理論在現代硬...
本書根據作者對計算機科學與技術專業教育特點的理解和“21世紀大學本科計算機專業系列教材”編寫的總體要求,作為《形式語言與自動機理論(第2版)》(主教材)一書的...
有限狀態自動機(FSM "finite state machine" 或者FSA "finite state automaton" )是為研究有限記憶體的計算過程和某些語言類而抽象出的一種計算模型。有限狀態自動機...
該書是關於形式語言、自動機理論和計算複雜性方面的經典教材,是三位理論計算大師的之作,現已更新到第3版。書中涵蓋了有窮自動機、正則表達式與語言、正則語言的...
下推自動機﹙PDA﹚是自動機理論中定義的一種抽象的計算模型。下推自動機比有限狀態自動機複雜:除了有限狀態組成部分外,還包括一個長度不受限制的棧;下推自動機的...
自動機編程(英語:Automata-based programming)是編程典範中的一種,是指程式或其中的部份是以有限狀態機(FSM)為模型的程式,有些程式則會用其他型式(也更複雜)的...
可計算理論中,計算模型很多, 如有窮自動機, 正則算法在本質上都與圖靈機相似。 Church-Turing 論題指出: 通常說的能行可計算函式等同於部分遞歸函式, 也等同於...
《形式語言與自動機理論教學參考書》是2013年清華大學出版社出版的圖書,作者是蔣宗禮。...
關於計算和計算機械的數學理論,也稱為計算理論或計算機科學的數學基礎。理論計算機科學主要包括:①自動機論與形式語言理論②程式理論③形式語義學④算法分析和計算複雜...
所謂的圖靈機就是指一個抽象的機器,它有一條無限長的紙帶,紙帶分成了一個一個...2. 蔣宗禮, 姜守旭.形式語言與自動機理論[M].2版.北京:清華大學出版社, 2007...
