基本介紹
- 中文名:有限狀態自動機
- 外文名:finite state machine
- 研究對象:自動機理論
- 識別語言:正規語言
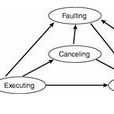
有限狀態自動機(FSM "finite state machine" 或者FSA "finite state automaton" )是為研究有限記憶體的計算過程和某些語言類而抽象出的一種計算模型。有限狀態自動機...
在計算理論中,確定有限狀態自動機或確定有限自動機(英語:deterministic finite automation, DFA)是一個能實現狀態轉移的自動機。對於一個給定的屬於該自動機的狀態和...
有限狀態機,(英語:Finite-state machine, FSM),又稱有限狀態自動機,簡稱狀態機,是表示有限個狀態以及在這些狀態之間的轉移和動作等行為的數學模型。...
在計算理論中,非確定有限狀態自動機或非確定有限自動機(NFA)是對每個狀態和輸入符號對可以有多個可能的下一個狀態的有限狀態自動機。...
在自動機理論(計算機科學的一個分支)中,確定有限狀態自動機最小化是將給定的確定有限狀態自動機(DFA, Deterministic Finite Automaton)改造為等價且擁有最少狀態的...
計算機控制系統的控制程式具有有限狀態自動機(FA)的特徵,可以用有限狀態機理論來描述。有限自動機(Finite Automata Machine)是計算機科學的重要基石,它在軟體開發領域...
《有限自動機理論》是2007年電子科技出版社出版的圖書,作者是陳文宇。...... 有限自動機(包括有限狀態自動機、下推自動機和圖靈機)的基礎理論,從構造文法產生語言的...
在計算理論中,米利型有限狀態機(英語:Mealy machine)是基於它的當前狀態和輸入生成輸出的有限狀態自動機(更精確的叫有限狀態變換器)。這意味著它的狀態圖將為每個...
Moore狀態機的輸出只與有限狀態自動機的當前狀態有關,與輸入信號的當前值無關。 Moore有限狀態機在時鐘CLOCK脈衝的有效邊沿後的有限個門延後,輸出達到穩定值。即使...
下推自動機﹙PDA﹚是自動機理論中定義的一種抽象的計算模型。下推自動機比有限狀態自動機複雜:除了有限狀態組成部分外,還包括一個長度不受限制的棧;下推自動機的...
自動機;用來描述通用計算機計算能力的圖靈機模型;進行與轉移函式,轉移狀態有關輸出的時序機;由一些基本語句構成程式框圖的波斯特機;隨即存儲機;堆疊自動機;不受有限...
它還可以被認為是沒有輸出只有輸入的有限狀態自動機。么半群理論的一個主要主張是半自動機等價於act;所以對於任何act,都有一個獨立的半自動機,或反過來說,對於...
自動機理論、語言和計算導論 第2版)John E.Hopcroft,Rajeev Motwani,Jeffrey D...本書主要內容包括:有限狀態自動機,正規語言,正規表達式,上下文無關文法,上下文無...
利用VC++6.0實現了給定文法所產生的句子、確定的有限自動機、不確定的有限自動機、帶空轉移的有限自動機、帶輸出的有限狀態自動機、下推自動機、確定的下推自動機...
表示層採用Web技術來實現,動作層採用Script Engine技術來實現,流程層採用有限狀態自動機來表現ATMC的套用流程。l 套用開發層:是由WSAPSDK構成,該平台是一個專業的...
詞法分析的第一階段即掃描器,通常基於有限狀態自動機。掃描器能夠識別其所能處理的標記中可能包含的所有字元序列(單個這樣的字元序列即前面所說的“語素”)。例如...
所以RASP有兩個“指令/程式”暫存器——(i)IR(有限狀態自動機的指令暫存器)和(ii)PC(程式計數器)用於位於暫存器中的程式。(同樣於專門的PC暫存器,RASP可以有專門...
