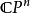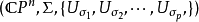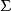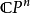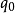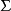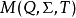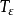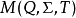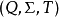基本介紹
- 中文名:半自動機
- 外文名:Semi-automatic machine
- 作用:么半群在集合上的乘法性運算
簡介,變換半群,M-acts,完全變換么半群,M-同態,性質,範疇Act,
簡介
半自動機是三元組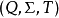 ,這裡的
,這裡的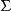 是叫做“輸入字母表”的非空集合,Q是叫做“狀態集合”的非空集合,而T是“轉移函式”,
是叫做“輸入字母表”的非空集合,Q是叫做“狀態集合”的非空集合,而T是“轉移函式”,
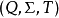
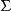
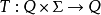
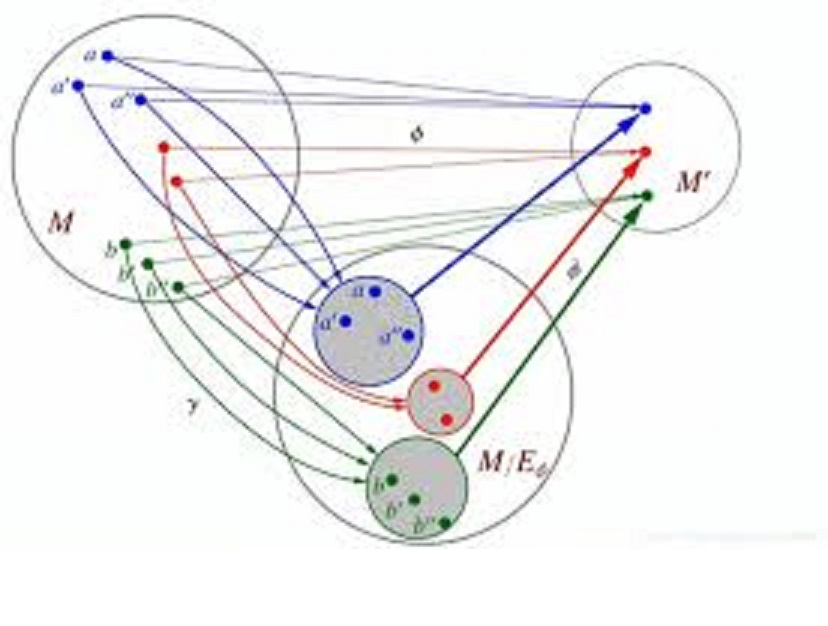
么半群理論的一個主要主張是半自動機等價於act;所以對於任何act,都有一個獨立的半自動機,或反過來說,對於任何半自動機,都有一個獨立的act。這可以如下這樣證實。
對於所有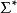 中的字w,設
中的字w,設 是如下遞歸定義的函式,對於所有Q中的q:
是如下遞歸定義的函式,對於所有Q中的q:
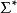


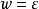

如果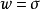 是
是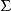 中的字母,則
中的字母,則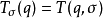 。
。
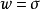
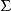
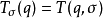
如果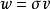 對於
對於 和
和 ,則
,則 。
。
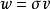



設 是個集合
是個集合

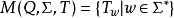
變換半群
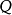










注意“半群”與“么半群”的使用:有些作者將“半群”與“么半群”視為同義詞。然而此處一個半群不必然包含單位元素;而一個么半群則意指含有單位元素的半群。因為作用於集合上的函式概念永遠包括恆等函式概念在內,亦即施加於集合上時不做任何動作,故變換半群可藉由與恆等函式聯集轉為么半群。
M-acts
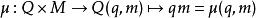
它滿足性質

此處1表么半群之單位元素,並且
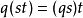
對所有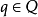 和
和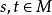 ,三元組
,三元組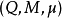 被稱為右
被稱為右 -act或簡稱右-act。一般而言,
-act或簡稱右-act。一般而言, 表示“
表示“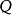 的元素與
的元素與 的元素的右乘法”。右-act經常寫為
的元素的右乘法”。右-act經常寫為 。
。
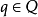
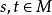
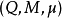


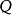


左-act定義類似,即
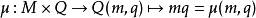
並經常表示為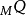 。
。
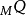
一個 -act變換半群十分相似,然而
-act變換半群十分相似,然而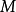 的元素本身不必然為函式,它們僅是某個么半群的元素。所以,必須限制
的元素本身不必然為函式,它們僅是某個么半群的元素。所以,必須限制 的作用與么半群中的乘法一致(亦即,
的作用與么半群中的乘法一致(亦即,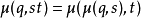 ),因為一般而言,對於某個任意
),因為一般而言,對於某個任意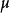 此性質可能不成立,保證此一致性可使進行函式複合時不致出問題。
此性質可能不成立,保證此一致性可使進行函式複合時不致出問題。

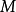

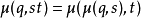
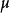
一旦加上這種限制,就可以完全放心的去掉所有括弧,因為么半群乘積和么半群在集合上的作用是完全滿足結合性的。特別是這允許了么半群的元素被表示為計算機科學意義上字母的字元串。這種抽象接著允許談論一般的字元串運算,並最終導致了由字母的字元串構成的形式語言概念。

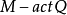
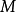
完全變換么半群
M-同態
M-同態是映射
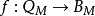
使得

對於所有 和
和 。所有M-同態的集合通常寫為
。所有M-同態的集合通常寫為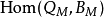 或
或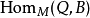 。
。


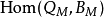
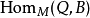
性質
如果狀態集合Q是有限的,則轉移函式通常表示為狀態轉移表。在自由群中字元串所驅動的所有可能轉移的構造有一種叫de Bruijn圖的圖形描述。