當遞推式中只含數列中的項,而無常數項或其它項時,就叫做遞歸公式。遞歸程式設計的公式化方法是一種簡單而有效的設計思想,它把程式設計和程式理解的難點都集中到遞歸公式上。由遞歸公式設計出的程式具有標準的分支結構,編寫和理解都要簡單的多。
基本介紹
- 中文名:遞歸公式
- 外文名:recursion formula
- 一級學科:數理科學
- 二級學科:數學
- 類型:數學術語
- 特點:特殊的遞推式
遞歸
遞推公式
遞歸公式簡介




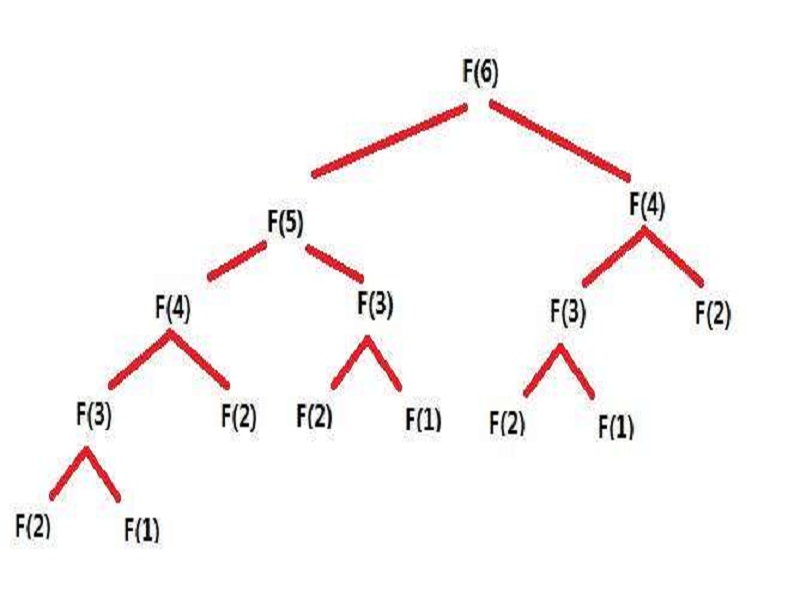
當遞推式中只含數列中的項,而無常數項或其它項時,就叫做遞歸公式。遞歸程式設計的公式化方法是一種簡單而有效的設計思想,它把程式設計和程式理解的難點都集中到遞歸公式上。由遞歸公式設計出的程式具有標準的分支結構,編寫和理解都要簡單的多。




當遞推式中只含數列中的項,而無常數項或其它項時,就叫做遞歸公式。遞歸程式設計的公式化方法是一種簡單而有效的設計思想,它把程式設計和程式理解的難點都集中到...
程式語言中,函式Func(Type a,……)直接或間接調用函式本身,則該函式稱為遞歸函式。遞歸函式不能定義為內聯函式。在數學上,關於遞歸函式的定義如下:對於某一函式...
遞歸算法(英語:recursion algorithm)在計算機科學中是指一種通過重複將問題分解為同類的子問題而解決問題的方法。遞歸式方法可以被用於解決很多的計算機科學問題,因此它...
遞歸定義是數理邏輯和計算機科學用到的一種定義方式,使用被定義對象的自身來為其下定義(簡單說就是自我複製的定義)。遞歸定義(recursive definition)亦稱歸納定義,一...
遞歸方法,是降格策略反映到數學思維中的一種方法,指從初始條件出發,利用遞推關係而求得一般結果的方法,例如降維法。...
遞歸調用是一種特殊的嵌套調用,是某個函式調用自己或者是調用其他函式後再次調用自己的,只要函式之間互相調用能產生循環的則一定是遞歸調用,遞歸調用一種解決方案,一...
程式調用自身的編程技巧稱為遞歸( recursion)。遞歸做為一種算法在程式設計語言中廣泛套用。 一個過程或函式在其定義或說明中有直接或間接調用自身的一種方法,它...
遞歸程式編輯 鎖定 問題如下。我們需要給予程式如階乘函式的定義以語義function factorial(n:Nat):Nat ≡ if (n==0)then 1 else n*factorial(n-1)。 這個...
遞歸做為一種算法在程式設計語言中廣泛套用。是指函式/過程/子程式在運行過程中直接或間接調用自身而產生的重入現象。遞歸是計算機科學的一個重要概念,遞歸的方法是...
遞歸語言是在形式語言字母表之上所有可能詞的集合中的遞歸集合。遞歸集合性質 編輯 如果A是遞歸集合,則A的補集是遞歸集合。 如果A和B是遞歸集合,則A∩B、A∪B...
一般遞歸模式稱為一般遞歸式,其中二為遞歸變元。...... 一般遞歸模式稱為一般遞歸式,其中二為遞歸變元。則稱f是由g,h,k依一般遞歸式定義的函式.上式稱為一般...
設(a0,a1,...,ar,...)是一個序列,把該序列中的ar和它前面的幾個ai(0≤i<r)關聯起來的方程稱做一個遞歸關係。如關係式:ar=3ar-1 (r≥1)和錯排數...
遞歸定理(recursion theorem)亦稱不動點定理。反映部分遞歸函式類基本性質的重要定理。最初是由美國邏輯學家、數學家克林(Kleene, S. C.)於1938年證明的,克林所...
所謂遞歸 ,籠統地說 ,是指運用收集到的知識作為行動的基礎去獲得更多的知識。由於這裡所涉及的往往是多個、甚至是無窮多個未知量 ,因此 ,所謂的遞歸事實上也就...
於是,丘奇的論題便成為:能行可計算的部分函式恰好是遞歸部分函式,而能行可計算的全函式也恰好是遞歸全函式,亦即一般遞歸函式。能行性和一般遞歸論題 編輯 ...
遞歸生成函式類(inductively generated classof function)是一種函式類。指從給定的函式出發,經過複合及一些遞歸運算元運算而得的全體函式組成的類.特別地,當生成運算元集...
互遞歸是數學與計算機科學中一種遞歸,指兩個數學或計算機對象如函式或數據類型互相定義。互遞歸在函式程式語言或某些問題域中非常常見,如遞歸下降分析器,其中數據類型...
超限遞歸定理(transfinite recursive theorem)是遞歸定理的推廣,該定理斷言:對任意函式F:V→V,存在惟一的函式G:ord→V,使得對任意α∈ord有G(α)=F(G|α),...
聯立遞歸式(simultaneous recursion schema )原始遞歸式的一種推廣形式.指同時定義多個函式而又不能獨立開來的一種函式定義方式.例如,給定函式A,B,C,D,由下列同時...
按一定次序排列的一列數稱為數列,而將數列{an} 的第n項用一個具體式子(含有參數n)表示出來,稱作該數列的通項公式。這正如函式的解析式一樣,通過代入具體的n...
遞歸論(Recursion theory)是數理邏輯的重要分支之一,研究解決問題的可行的計算方法和計算的複雜程度的一門學科,尤其是研究遞歸函式及其推廣。遞歸論研究的函式主要包括...
遞歸可枚舉集,又稱部分遞歸集。在能行性理論中,基本概念是遞歸函式,它可刻畫為:任給x,只要它在x處有定義必可在有限步驟內求出其值。因此遞歸全函式(即處處有...
遞歸集是遞歸論用語。令A⊆Nn,如果A的特徵函式CA(x1,…,xn)是μ-遞歸函式,則稱A為遞歸集。 遞歸論又稱“遞歸函式論”、“能行性理論”,指主要用數學方法...
1、謂詞合式公式的定義在謂詞演算中合適公式的遞歸定義如下:(1) 原子謂詞公式是。(2) 若A為合式公式,則~A也是一個合式公式。(3) 若A和B都是合式公式,...
詞語解釋 按照某一包含有限步數的法則或公式對一個或多個前面的元素進行運算,以確定一系列元素(如數或函式)的方法 ...
這些函式也叫做偏遞歸函式。在可計算理論中,函式的定義域是函式被定義在其上的所有輸入的集合。 [2] 定義在所有參數上的函式叫做全函式。如果可計算函式是全函式...
