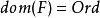超限歸納法

超限歸納法又稱超窮歸納法、超限歸納證法，數學中用來證明某種類型命題的重要方法。

基本介紹

• 中文名：超限歸納法
• 外文名：transfinite induction
• 別稱：超窮歸納法、超限歸納證法
• 學科：數理科學

介紹

超限歸納法（transfinite induction）是數學歸納法向（大）良序集合比如基數或序數的集合的擴展。

超限歸納

假設只要對於所有的 β < α，P(β) 為真，則 P(α) 也為真。那么超限歸納告訴我們 P 對於所有序數為真。

就是說，如果 P(α) 為真只要 P(β) 對於所有 β < α 為真，則 P(α) 對於所有 α 為真。或者更實用的說：若要證明所有序數 α 都符合性質 P，你可以假定它對於所有更小的 β < α 已經是成立的。

通常證明被分為三種情況：

• 零情況：證明 P(0) 為真。
• 後繼情況：證明對於任何後繼序數β+1， P(β+1) 得出自 P(β)（如果需要的話，也假定對於所有 α < β 有 P(α)）。
• 極限情況：證明對於任何極限序數λ, P(λ) 得出自 [P(α) 對於所有 α < λ]。

留意，以上三種情況(證明方法)都是相同的，只是所考慮的序數類型不同。正式來說不用分開考慮它們，但在實踐時，因為它們的證明過程通常相差很大，所以需要分別表述。在一些情況下，“零情況”會被視為一種“極限情況”，因此可以使用極限序數來證明。

超限遞歸

超限遞歸是一種構造或定義某種對象的方法，它與超限歸納的概念密切相關。例如，可以定義以序數為下標的集合序列A_α，只要指定三個事項：

• A₀是什麼
• 如何確定A_α+1自A_α（又或者是從A₀到A_α的部分）
• 對於極限序數 λ，如何確定A_λ自A_α的對於 α < λ 的序列。

更形式的說，我們陳述超限遞歸定理如下。給定函式類G₁,G₂,G₃，存在一個唯一的超限序列F帶有 （ 是所有序數的真類），使得

，對於所有

，對於所有極限序數。這裡的是指F在上的限制。

注意我們要求G₁,G₂,G₃的定義域足夠廣闊來使上述性質有意義。所以滿足這些性質的序列的唯一性可以使用超限歸納證明。

更一般的說，你可以在任何良基關係R上通過超限遞歸定義對象。（R甚至不需要是集合；它可以是真類，只要它是類似集合的關係便可，也就是說：對於任何x，使得yRx的所有y的蒐集必定是集合。）

同選擇公理的聯繫

有一個常見的誤解是超限歸納法或超限遞歸法要求選擇公理。其實超限歸納可以套用於任何良序集合。但是常見的情況是使用選擇公理來良序排序一個集合，使其適用超限歸納法。

套用

超限歸納法是數學歸納法的形式之一，可以套用於（大的）良序集，比如說套用到序數或基數，甚至於所有有序的集。

超限歸納法可用於證明一個命題P在所有序數中成立：

基礎：證明P(0)成立；

歸納：證明對於任何一個序數b，如果P(a)在所有序數a<b中成立，那么P(b)也將成立。

後面一步常常分解為兩種情況：

能套用和一般的歸納法相似的方法的後繼序數（有直接前驅的序數），（P(a)蘊涵P(a+1)），

沒有前驅的極限序數，因此不能用這種方法。

顯然，極限序數可以通過將極限序數b看成所有小於b的序數的極限來處理：假定在所有的a<b中P(a)成立，取所有這些情況的極限（通常通過並集公理實現），則證明了P(b)。