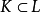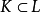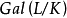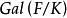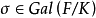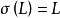正規閉包(normal closure)是一種特殊的正規子群,群中包含某個子集的最小正規子群。代數擴張K/F稱為正規擴張,是指F[X]中每個在K中有根的既約多項式,在K[X]中可以分解為一次因子的乘積,它等價於K的任意元α在F上的最小多項式在K[x]中可以分解為一次因子的乘積。一個代數擴張K/F的正規閉包是指F的一個正規擴張,它包含K且它包含的K的任意真子域在F上都不是正規的。
基本介紹
- 中文名:正規閉包
- 外文名:normal closure
- 屬性:一種特殊的正規子群
- 所屬學科:數學(群論基礎)
- 相關概念:正規擴張,多項式的分裂域等
基本介紹,相關定義及定理,
基本介紹
正規擴張(normal extension)是一種重要的代數擴張,它與多項式的分裂域密切相關,代數擴張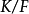 稱為正規擴張,是指
稱為正規擴張,是指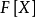 中每個在
中每個在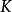 中有根的既約多項式,在
中有根的既約多項式,在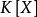 中可以分解為一次因子的乘積,它等價於
中可以分解為一次因子的乘積,它等價於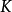 的任意元
的任意元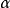 在
在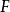 上的最小多項式在
上的最小多項式在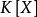 中可以分解為一次因子的乘積。一個代數擴張
中可以分解為一次因子的乘積。一個代數擴張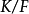 的正規閉包是指
的正規閉包是指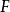 的一個正規擴張,它包含
的一個正規擴張,它包含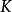 且它包含的
且它包含的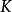 的任意真子域在
的任意真子域在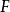 上都不是正規的。值得注意的是,即使
上都不是正規的。值得注意的是,即使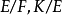 是正規擴張,也不能推出
是正規擴張,也不能推出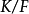 是正規的。例如,對域鏈
是正規的。例如,對域鏈
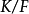
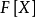
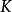
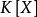
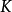
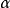
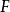
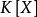
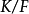
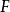
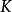
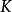
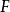
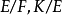
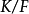
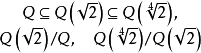
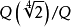
相關定義及定理
定義1 設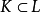 為域擴張,
為域擴張,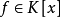 ,如果
,如果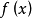 在
在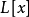 中完全分解為一次因子的積,則稱
中完全分解為一次因子的積,則稱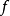 在
在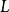 中分裂。
中分裂。
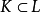
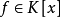
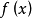
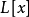
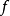
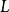
定義2 一個域擴張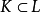 稱作正規的,如果
稱作正規的,如果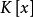 中的任一不可約多項式若在
中的任一不可約多項式若在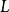 中有零點則在
中有零點則在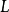 中分裂。
中分裂。
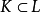
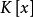
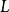
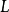
命題1 對一個有限域擴張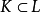 ,下列三條件等價:
,下列三條件等價:
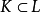
i) L是K的正規擴域;
ii) L是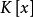 中一個多項式的分裂域;
中一個多項式的分裂域;
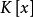
iii) 對任一域擴張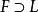 及任意
及任意 。
。
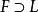

注1 對無限代數擴張,只要將ii)中的“一個多項式”改為“一組多項式”,命題1仍成立(在多項式個數不可數的情形需要用超限歸納法證明)。
定義3 設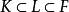 為域擴張,其中F是K的正規擴域,如果F的任一包含L的真子域都不是K的正規擴域,則稱F為L在K上的一個正規閉包(直觀地說它是K的包含L的最小正規擴張)。
為域擴張,其中F是K的正規擴域,如果F的任一包含L的真子域都不是K的正規擴域,則稱F為L在K上的一個正規閉包(直觀地說它是K的包含L的最小正規擴張)。
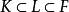
推論1 對任意代數擴張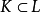 存在正規閉包F,它是L中所有元在K上的定義多項式的一個分裂域,且
存在正規閉包F,它是L中所有元在K上的定義多項式的一個分裂域,且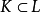 的正規閉包在
的正規閉包在 -代數同構之下是唯一的。此外,任意
-代數同構之下是唯一的。此外,任意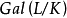 的元可以擴張為
的元可以擴張為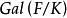 的元。
的元。