塞瓦定理

塞瓦定理是指在△ABC內任取一點O，延長AO、BO、CO分別交對邊於D、E、F，則 (BD/DC)×(CE/EA)×(AF/FB)=1。

塞瓦(Giovanni Ceva，1648~1734)義大利水利工程師，數學家。塞瓦定理載於塞瓦於1678年發表的《直線論》一書，也有書中說塞瓦定理是塞瓦重大發現。

塞瓦定理記憶方法：三頂點選一個作為起點，定一方向，繞一圈，三組比例相乘為一。

基本介紹

• 中文名：塞瓦定理
• 外文名：Ceva's theorem
• 表達式： (BD/DC)×(CE/EA)×(AF/FB)=1
• 提出者：喬瓦尼·塞瓦
• 提出時間：1678年
• 適用領域：平面幾何
• 套用學科：數學、物理
• 提出者國家：義大利

證明推導

（1）本定理可利用梅涅勞斯定理(梅氏定理)證明：

∵△ADC被直線BOE所截，

①

∵△ABD被直線COF所截，

②

②/①約分得：

（2）也可以利用面積關係證明（燕尾定理）

③

同理 ④ ，⑤

③×④×⑤得

定理的推廣

①證明三角形三條高線必交於一點:

設△ABC三邊的高分別為AE、BF、CD，垂足分別為D、E、F，根據塞瓦定理逆定理，因為，所以三條高CD、AE、BF交於一點。

或者用塞瓦定理的角元形式證明，證明如下:

由"同角的餘角相等"可得，

,

所以三條高CD、AE、BF交於一點。

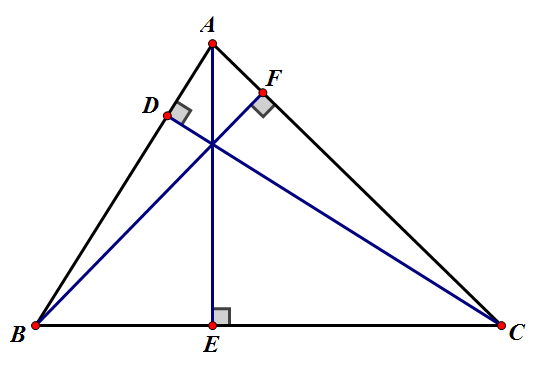
圖1塞瓦定理證明三條高交於一點

②三角形三條中線交於一點（重心）:

如圖1：已知，D、E分別為△ABC的邊BC、AC 的中點，連線AD、BE相交於點O，連線CO並延長交AB於F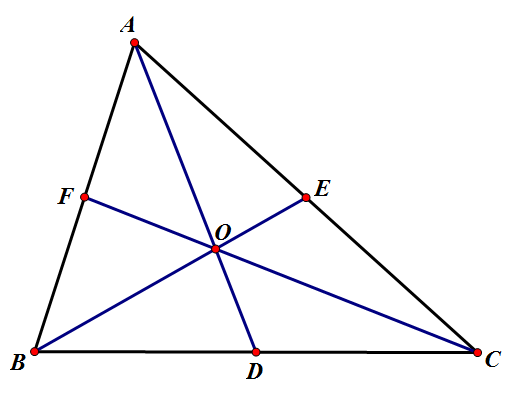

圖2塞瓦定理證明三條中線交於一點

求證：

證明：

由塞瓦定理得

∴CF為AB邊上的中線

∴三角形三條中線交於一點（重心）

③用塞瓦定理證明三條角平分線交於一點

如圖1，

此外，可用定比分點來定義塞瓦定理：

在△ABC的三邊BC、CA、AB或其延長線上分別取L、M、N三點，又分比是。於是AL、BM、CN三線交於一點的充要條件是。（注意與梅涅勞斯定理相區分，那裡是）

推論

1.塞瓦定理角元形式

AD,BE,CF交於一點的充分必要條件是：

(簡記為不相鄰三條線段所對角的正弦值之積等於另外三條線段)

由正弦定理及三角形面積公式易證。

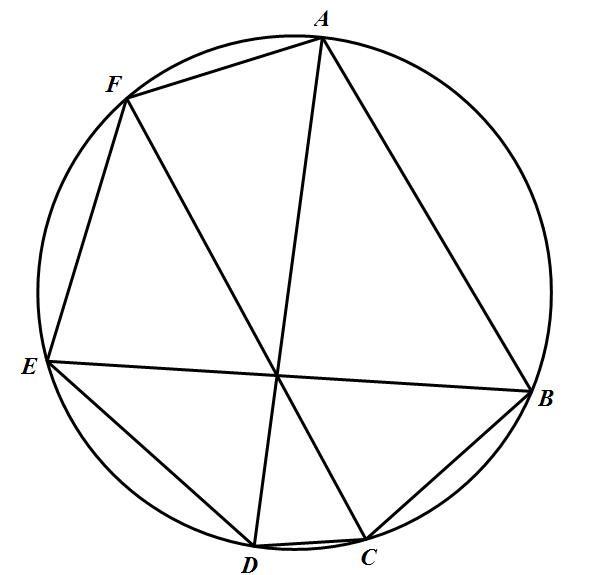
2.如圖2，對於圓周上順次6點A，B，C，D，E，F，直線AD，BE，CF交於一點的充分必要條件是：

由塞瓦定理的角元形式，正弦定理及圓弦長與所對圓周角關係易證

圖2

數學意義

使用塞瓦定理可以進行直線形中線段長度比例的計算，其逆定理還可以用來進行三點共線、三線共點等問題的判定方法，是平面幾何學以及射影幾何學中的一項基本定理，具有重要的作用。塞瓦定理的對偶定理是梅涅勞斯定理。

記憶方法

塞瓦定理的優點多多，但是卻不是特別好記，這裡有一個方法。

相當於

可以發現,左右兩端字母一樣

可以作如下表述，在記憶時，可理解為在符合在三邊線段的前提下，分母分子字母一樣，且分母、分子內部有相同字母.。

另外一種記憶方式是，將圖2中的ABC作為頂點，圖2中的DEF作為分點，則可以看做是：頂點到分點（BD），該分點到另一頂點（DC），頂點再到分點（CE），分點再到頂點（EA），頂點再到分點（AF），分點再到頂點（FB）。