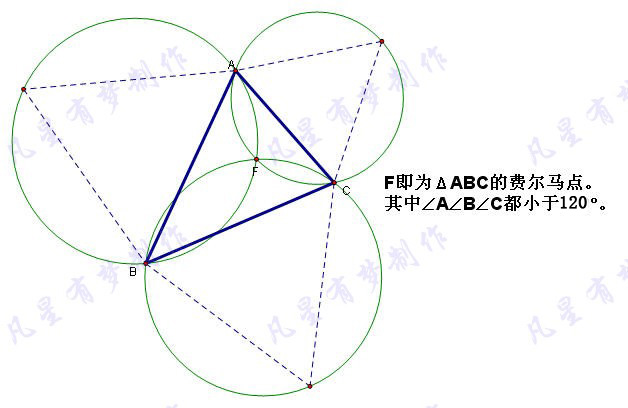
費爾馬點——就是到三角形的三個頂點的距離之和最短的點。 對於一個頂角不超過120度的三角形,費爾馬點是對各邊的張角都是120度的點。 對於一個頂角超過120度的三角形,費爾馬點就是最大的內角的頂點。
基本介紹
- 中文名:費爾馬點
- 國籍:法國
- 出生日期:1601年8月17日
- 逝世日期:1665年1月12日
- 主要成就:費爾馬大定理;費爾馬點
- 領域:數學
- 相關人物:費爾馬
- 產生時間:15世紀
費爾馬,報告記載,學習經歷,貢獻,費爾馬的研究趨向,費爾馬的猜想,費爾馬的發現,問題,證明方法,機率成為學科,
費爾馬
在笛卡兒系統地闡述現代解析幾何基礎的同時,另一位法國數學天才費爾馬(Pierrede Fermat)也注意到這門學科.費爾馬要求承認是他發明解析幾何的理由是:他在1536年9月給羅伯瓦的一封信中說到,他有這個概念已經七年了.在他死後發表的論著《平面和立體的軌跡引論》(isogoge ad locus planos et solidos)中,記載了這項工作的一些細節.在這裡,我們見到了一般直線和圓的方程,以及關於雙曲線、橢圓、拋物線的討論.在一部1637年前完成的、關於切線和求面積的著作中,費爾馬解析地定義了許多新的曲線.笛卡兒只提出了很少幾種由機械運動生成的新曲線,而費爾馬則提出了許多以代數方程定義的新曲線.曲線xmyn=a,yn=axm和rn=aθ,還被稱作費爾馬的雙曲線(hyperbolas)、拋物線(parabolas)和螺線(spirals of Fermat).費爾馬還和別人一起提出了後來被稱作阿涅澤的箕舌線(witch of Agnesi)的三次曲線;這曲線是以阿涅澤(Mati- a Haetana Agnesi,1718—1799)的名字命名的,她是一位多才多藝的婦女,是傑出的數學家、語言學家、哲學家和夜遊病患者.這樣,在很大程度上,笛卡兒從一個軌跡開始然後找它的方程,費爾馬則從方程出後,然後來研究軌跡.這正是解析幾何的基本原則的兩個相反的方面.費爾馬的著作用的是韋達的記號,並且因此,與笛卡兒的較為現代的記號相比,有點象古文.
報告記載
有一個看來可靠的報告說,費爾馬在1501年8月17日出生於土魯斯附近的博芒特.德.洛馬格內.他在1565年1月12日死於卡斯特爾或土魯斯,這是人們都知道的.他的墓碑,原來在土魯斯的奧古斯丁教堂,後來移到當地的博物館;在墓碑上寫著上述的死的日期和死時的年齡:五十七歲.但是,這與通常標出的費爾馬生卒年(1501—1565)相牴觸.事實上,不同的作者對費爾馬的出生年有不同的說法(當然都有其理由):從1500年到1668年,不等.
學習經歷
費爾馬是一個皮革商的兒子,童年是在家裡受的教育.三十歲,他得到土魯斯地方議會辯護士的職位.在那裡,他謙虛謹慎地乾他的工作.他在當卑微的律師時,把自己大量的業餘時間用於數學研究.雖然他一輩子發表的著作不多,但他和同時代的許多第一流數學家有科學上的通信關係,並且以這種方式給他的同行以相當大的影響.他以那么多的重要貢獻豐富了那么多的數學分支,以致曾被稱作十五世紀法國偉大的業餘數學家.
貢獻
費爾馬的研究趨向
1.如果p是素數,並且a與p互素,則a↗(p-1)-1(a的(p-1)次冪減1)可被p整除.例如,如果p=5,a=2,a↗(p-1)-1=15=(5)(3).此定理被稱作費爾馬小定理(little Fermat theo-rem),是費爾馬在1640年10月18日給德貝西(Frenicle de Bessy)的信中給出的,未作證明.歐拉於1736年發表了第一個關於費爾馬小定理的證明。
另一方面,如果p=x2-y2,則p=(x+y)(x-y).但是,因為p是素數,它只有因數p和1.因此,x+y=p和x-y=1,或x=(p+1)/2和y=(p-1)/2.
3.一個形式為4n+1的素數可以表成兩個平方數之和.例如,5=4+1,13=9+4,17=16+1,29=25+4.此定理是費爾馬在1640年12月25日給梅森的信中最先指出的.歐拉於1754年首先證明了它,並且還證明了這種表達式的唯一性.
4.一個形式為4n+1的素數,作為整數邊直角三角形的斜邊,僅有一次;其平方有兩次;其立方有三次,等等.例如,5=4(1)+1,這時有52=32+42;252=152+202=72+242;1252=752+1002=352+1202=442+1172.
6.整數邊直角三角形的面積不能是一個平方數.這也是後來由拉格朗日證明的.
7.x2+2=y3隻有一個整數解;x2+4=y3隻有兩個整數解.這是向英國數學家們提出的一個競賽題.第一個方程的解是x=5,y=3;第二個方程的解是x=2,y=2和x=11,y=5.
8.不存在正整數x,y,z,使得x^4+y^4=z2.
9.不存在正整數x,y,z,n,使得xn+yn=zn(當n>2時).這個著名的猜想,稱為費爾馬最後“定理”(Fermat’s last“theorem”).費爾馬把它寫在丟番圖的梅齊利亞克譯本的手抄本第二卷問題8的旁邊,這個問題是:“分一給定的平方數為兩個平方數.”費爾馬的頁邊評註斷定:“分一立方數為兩個立方數,分一個四次冪(或者一般地,任何次冪)為兩個同次冪,即a的平方加b的平方等於c的平方中a,b,c都沒有整數解,這是不可能的:我確實找到了一個巧妙的證明方法,但是頁邊太窄,寫不下了.”費爾馬是否真有此問題的一個完善的證明,也許將永遠是個謎!從那時起,許多卓越的數學家曾在此問題上試驗他的技巧,但是這一般的猜想,至今仍然期待人們去解決.在別處,費爾馬對n=4的情況給出了一個證明:歐拉給出了一個n=3的情況的證明(後來由別人加以完善).大約1825年,勒讓德和狄利克雷獨立地對於n=5的情況給出了證明;拉梅於1839年對於n=7證明了此定理.德國數學家庫默爾(E.Kummet.1810—1893)對此問題的研究作了有意義的推進.1843年,庫默爾向狄利克雷提交了一個書面說明,後者指出了其推理中的一個錯誤.庫默爾回過來重新研究它,又過了幾年,日本一位數學家假設,若n大於等於3而小於等於20時,a,b,c沒有整數解。這時在稱作理想數理論(The theory of ideals)的高等代數中發展了一個與之相聯繫的重要課題,為費爾馬關係式的不可解性導出很一般的條件.現在知道:費爾馬的最後“定理”,對於n<125000和許多別的特殊的n值,確實成立.1908年,德國數學家瓦爾夫斯克爾給哥廷根科學院留下十萬馬克,作為這個“定理”的第一個完全證明的獎金.結果,追求名利者提出的證明紛至沓來,並且從那以後,這個問題的業餘愛好者簡直到處都有,就象對於三等分角和化圓為方問題一樣,費爾馬的最後“定理”作為數學問題而享有盛名,原因就在於:對於它,已經發表了許多錯誤證明.
費爾馬的猜想
對於所有非負數n,f(n)=22n+1是素數.這個猜想已被證明是錯誤的;歐拉證明了:f(5)是合數.已知:對於5≤n≤16和n的至少四十七個其它值(也許最大的是n=1945),f(n)是合數.f(5),f(6)和f(8)的素因子已找到;f(9)的一個素因子已找到.
費爾馬的發現
1879年,在萊頓的圖書館中,在C.惠更斯手稿中間,發現一篇論文,其中,費爾馬講到一種一般方法——他可能曾用它作出他的許多發現.這方法被稱作費爾馬的無限遞降法(method of infinite descent)對於確立否定的結論很有用.這方法,簡單地說,是這樣的:為了證明與正整數相聯繫的某關係式是不可能的,假定:反過來,該關係式被一些正整數的特定集合滿足.從這假定出發,證明:同樣的關係式對另一較小的正整數的集合成立.於是,再用同方法證明:該關係式對於另一個更小的正整數集合成立,等等以至無窮.因為正整數不能無限減小,所以,開始的假定是站不住腳的,因而,原來的關係式不能成立.為了弄清這b是正整數.
問題
我們已經講過,帕斯卡與費爾馬的通訊關係為機率論奠了基.應該記得:它是從所謂得分問題(problem or the points)開始的:“在兩個被假定有同等技巧的博弈者之間,在一個中斷的博弈中,如何來確定賭金的劃分,已知兩個博弈者在中斷時的得分及在博弈中獲勝所需要的分數.”費爾馬討論了一個博弈者A需要2分獲勝,另一個博弈者B需要3分獲勝的情況.這是費爾馬對於此種特殊情況的解.因為,顯然最多四次就能決定勝負,令a表示A勝,b表示B勝,考慮a和b兩個字母每次取4個的16種排列:
aaaa aaab abba bbab
baaa bbaa abab babb
abaa baba aabb abbb
aaba baab bbba bbbb
證明方法
a出現等於或多於2次,則A獲勝:有11種情況是這樣的.b出現等於或多於3次,則B獲勝;有5種情況是這樣的.所以,賭金應以11∶5的比例劃分.對於一般情況:A需要m分獲勝,B需要n分獲勝,我們能寫出a、b兩個字母每次取m+n-1個的2m+n-1種排列.然後,我們找a出現等於或多於m次的α種情況,和b出現等於或多於n次的β種情況.所以,賭金應以α∶β的比例劃分.
帕斯卡利用其“算術三角形”解得分問題,在9.9節中講過.令C(n,r)表示從n件中每次取r件的組合數[參看問題研究9.13(g)],我們能容易地證明:“算術三角形”的第五條對角線上的數分別為:
C(4,4)=1,C(4,3)=4,C(4,2)=6,C(4,1)=4,C(4,0)=1.
因為,回到上面講的特殊的得分問題,C(4,4)是得4個a的方式數,C(4,3)是得3個a的方式數,等等;由此得出:此問題的解為:
[C(4,4)+C(4,3)+C(4,2)]∶[C(4,1)+C(4,0)]=(1+4+6)∶(4+1)
=11∶5
對於一般情況,A需要m分獲勝,B需要n分獲勝,我們選擇帕斯卡算術陣的第(m+n)條對角線.然後,我們求此對角線的前n個數的和α和此對角線的最後m個數的和β.於是,賭金應依α∶β的比例劃分.
帕斯卡和費爾馬在他們1654年的有歷史意義的通信中考慮到有關得分問題的其它問題,例如,當博弈者超過兩個時,或兩個博弈者的技巧參差不齊時,賭金該如何劃分.帕斯卡和費爾馬的這個工作開數學機率論之先河.惠更斯(Christiaan Huygens,1629—1695)寫關於機率論的第一篇正式論文,就是以帕斯卡—費爾馬的通信為基礎的.雅科布.伯努利(Jakob Bernoulli,1654—1705)的《猜測術》(Ars conjectandi)在他死後1713年才出版;這部書是這門學科的最優講述,它包括惠更斯的較早的論文.繼這些先行者之後,促進此學科發展的有:棣莫費爾(De Moivre,1667—1754),丹尼爾.伯努利(Daniel Bemoul-li,1700—1782),歐拉(1707—1783),拉格朗日(1736—1813),拉普拉斯(1749—1827),和一大批其他數學家.
機率成為學科
引人入勝並且有些令人驚異的是:數學家們居然有能力發展這樣一門學科(即,數學機率論),它證明的理性的定律能被套用於純屬機遇的場合.這門學科遠不是不實際的:通過大試驗室中進行的實驗,通過與機率有密切關係的保險公司的存在,並通過大商業和戰爭的推理計算,表明了這一點.