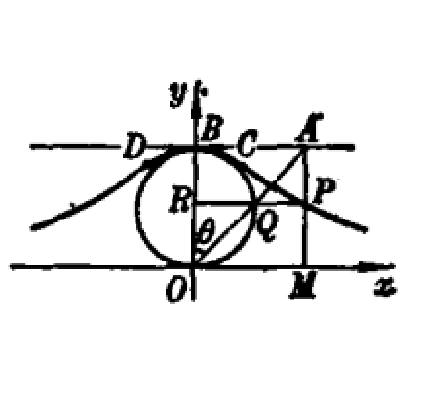
自定圓x2+y2-ay=0上一定點O(0，0)作任意直線，分別交直線y=a於A點，交圓於Q點；過Q、A分別作x，y軸的平行線相交於P點，則P點的軌跡稱為箕舌線(witch)。
基本介紹
- 中文名：箕舌線
- 外文名：Witch/versiera
- 屬性：平面曲線的一種
- 所屬學科：數學
- 所屬問題：平面解析幾何(平面曲線)
- 別名：阿涅西箕舌線
定義,箕舌線的方程,相關性質,起源,
定義
過原點的動直線交定圓
於P點，交直線
於
點，過
和分別作
軸和
軸的平行線交於M點，則M點的軌跡叫做箕舌線。
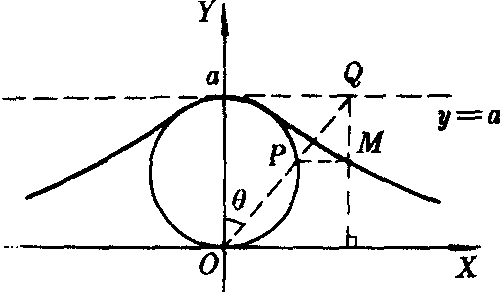圖1箕舌線的方程
箕舌線的方程是：
參數方程是：
相關性質
設定圓直徑為
，箕舌線有漸近線
，曲線與漸近線之間的面積為
，
，極大點為
，在該點的曲率半徑為
。有拐點
，在這兩點處的切線斜率分別為
。過曲線上任一點M作
交圓於P，則有
。女數學家阿涅西(M.G.Agnesi)對箕舌線作了詳細的研究，故又稱箕舌線為阿涅西箕舌線。費馬(P.deFermat)和格蘭迪(G.Grandi)早已知道這種曲線。
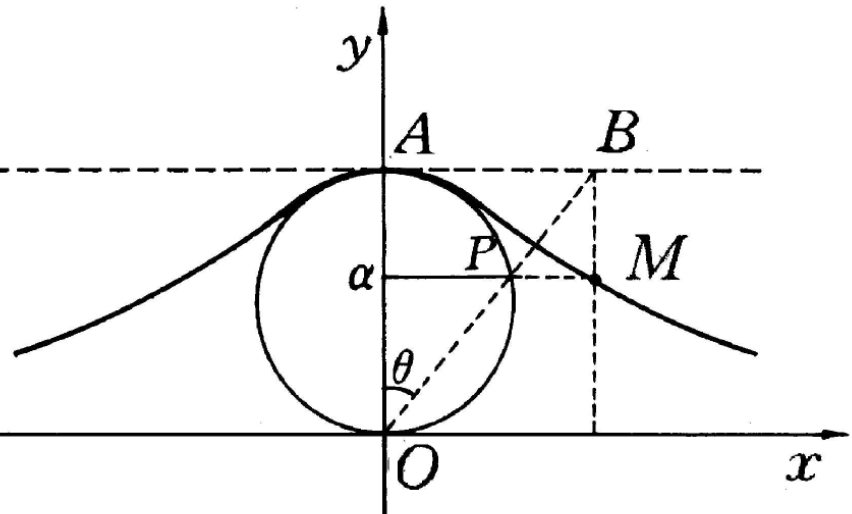圖2起源
“阿涅西箕舌線”的名字來源於瑪麗亞·阿涅西(1718-1799)，這是一位極有天賦的義大利數學家，1748年她的一篇關於微積分和解析幾何的長文發表在《分析講義》上(崔西戴爾(C.Truesdell)，1989)。她討論了這個曲線及其一些數學特性，並稱它為“la Versiera”，義大利語意指“巫婆”或“女妖”。但是阿涅西不是第一個使用“Versiera”這個詞語的人，蓋多·格蘭迪(1671-1743)在1718年已經使用過該術語，在說明一個來源於“seni versi”，即正矢(譯者註：即為函式
)的曲線時，模仿拉丁單詞“Versoria”而稱之為“Versiera”(勞瑞(G.Loria)，1930，PP.93-99)。然而一些人解釋“Versoria”就是正矢，那時字典里唯一與“Versoria”相關的解釋是“旋轉或扭曲”。由於“Versiera”不是義大利語中的“Versoria”，而是“avversario”的陰性詞，有時用來表示惡魔，因此格蘭迪也許在玩一個文字遊戲。或者由於義大利單詞“seno”是胸部的意思，與正弦一樣，也許他綜合考慮了其他問題。格蘭迪對柯西密度的構建非常簡單，可以輕鬆用來提高這個曲線現代素描的質量(圖3)。牛頓在1718年之前已經給出相同的圖解，但是直到1799年才被印刷出版。
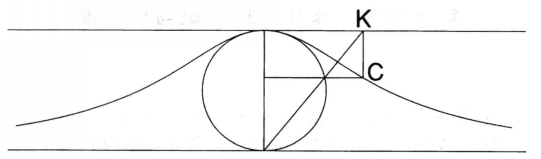圖3
