基本介紹
緒論,定義,套用,
緒論
定義
固定正整數g,N。首先定義西格爾上半平面為
再定義一個離散子群
再設
現在可以定義西格爾模形式:對任一函式 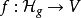 ,我們採用下述符號
,我們採用下述符號
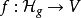
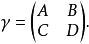
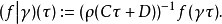
所謂權為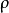 、次數為g、階為N 的西格爾模形式,是滿足下述條件的全純函式
、次數為g、階為N 的西格爾模形式,是滿足下述條件的全純函式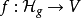 :
:
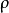
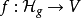
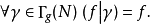
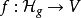
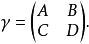
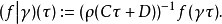
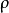
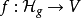
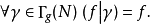
在數學中,西格爾模形式是辛群上的自守形式。西格爾模形式是西格爾上半平面上的一類多變元全純函式,模形式是其特例。...
希爾伯特模形式是一種模形式概念的推廣。關於希爾伯特模形式也有類似於模形式、西格爾模形式等情形的結果。模形式論是一種特殊的自守形式的理論。由(J.-)H.龐加...
,便得到西格爾模形式。模形式與橢圓曲線相關,而西格爾模形式則涉及更廣義的阿貝爾簇。自守形式的概念可用於一般的李群。參考資料 1. [1]朱學勇. 格的極值問題的...
奇異形式(singular modular form)一個西格爾模形式.其傅立葉係數a (t)對半整、正定的t是零。設f是n階西格爾模形式,權是k.當kGn/2(此時稱k為奇異權)時,f...
數論中的希爾伯特模形式和一些函式在許多上半平面組成的空間H有關。另一個數論研究者感興趣的空間是西格爾上半平面Hn,是西格爾模形式的定義域。...
在模形式方面,亦有例如希爾伯特模形式、西格爾模形式和theta-級數等等面向。朗蘭茲綱領起因 編輯 洛朗·拉佛閣在朗蘭茲綱領研究方面取得了巨大的進展,他證明了與...
