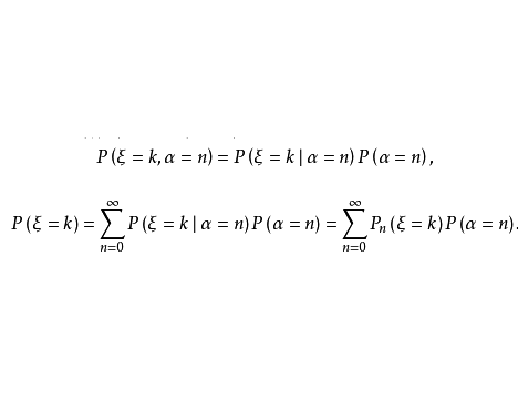
複合分布，是一類機率分布，如果一個隨機變數ξ服從的分布與一個參數α有關，而α也是一個隨機變數，α服從一個確定的分布，這時稱隨機變數ξ服從一個複合分布。例如，複合二項分布、複合泊松分布、複合負二項分布等。基本介紹複合分布是...
《複合分散式》是2019年12月中國海洋大學出版社出版的圖書，作者是陳柏宇，劉桂林，王莉萍。內容簡介 本書以測度論為基礎，在嚴謹的數學理論基礎上，建立了一個由離散型隨機變數和一個多維連續型隨機變數構成的一種新型的理論分布模型——...
對合分布(involutive distribution)是一類特殊的分布。黎曼幾何的重要概念。指微分流形切叢的一個子叢。黎曼幾何是微分幾何的一個重要分支，由德國數學家黎曼(Riemann，(G.F.)B.)於19世紀中期所開創。他於1854年在哥丁根大學所做的就職...
《山楊複合體的地理分布變遷動態歷史研究》是依託四川大學，由毛康珊擔任項目負責人的面上項目。項目摘要 溫帶植被，尤其是林木物種，對第四紀氣候變化和未來氣候變化的回響是一個經典的生物地理學議題。林木物種一般通過地理分布範圍變遷和局...
複合泊松過程(compound Poisson process)一類隨機過程。是由對泊松過程的每一點賦予一獨立同分布的隨機變數而得的隨機過程.對於隨機過程{X(t),t≥0}如果對任意t≥0,它能表為其中{N(t),t≥0}是一泊松過程,而{Y ,n=1,2,......
（2）複合地層在水平方向上的變化。在一施工段當中，可能分布著不同時代、不同岩性、不同風化程度或不同層序的地層，從而表現出水平方向上工程地質性質的差異。特殊的複合地層 還有一些不良地質，屬於特殊的複合地層，盾構施工遇到需要採取...
是不同群落之間水平分布格局的一個特徵。在森林-草原、草原-荒漠等植被過渡地帶，常常有明顯的表現。特點 群落複合體是由於地形條件起伏的變化，引起土壤水分、肥力、甚至鹽分等生態因子的交替變化，而導致兩個以上的植物群落（往往是群落...
與此同時，光子晶體的空間分布、介質材料的介電常數、光子晶體的周期結構以及光子晶體缺陷的設定是影響光子晶體濾波器性能的主要因素。基於以上分析，本文將點缺陷與環形腔相結合，通過複合缺陷實現了濾波器結構的設計，實現了特定波長的濾波...
《螺旋磁場連鑄複合材料及顆粒分布模型研究》是依託大連理工大學,由張維平擔任項目負責人的青年科學基金項目。項目摘要 金屬基複合材料的高質量、低成本、規模化是其得到廣泛套用的基礎。本項目研究了用電磁攪拌器代替機械攪拌器連續鑄造金屬基...
(i) 複合材料必須是人造的，是人們根據需要設計製造的材料;(ii) 複合材料必須由兩種或兩種以上化學、物理性質不同的材料組分，以所設計的形式、比例、分布組合而成，各組分之間有明顯的界面存在;(iii)它具有結構可設計性，可進行複合...
正因為它具有實木地板的各種優點，擯棄了強化複合地板的不足，又節約了大量優質珍貴木材資源。由三層實木交錯層壓而成，有效地改良了木材易變形、翹曲和開裂等不足。分布情況 實木複合地板一般可分為三層實木複合地板、多層實木複合地板和細...
2、交界痣痣細胞在表皮和真皮交界處，呈多個巢團狀，邊界清楚，分布距離均勻；每個巢內的上一半在表皮的底層，內下一半則在真皮淺層內，這些痣細胞為大痣細胞色素較深 。3、複合痣在痣細胞進入真皮的過程容易中，常同時有皮內痣和...
或地塊複合於構造帶之上。構造複合現象的分析和研究，對區域構造格局形成及發展過程乃至劃分構造體系都是十分重要的。越來越多的資料表明，各類礦產的形成與分布的規律多與構造複合現象關係密切，對於區域穩定性與地質災害研究都有現實意義。
利用地物因時間推移產生的動態變化，通過不同時相信息複合可探測地物動態特徵。如湖泊水位消漲、河道演變、颱風路徑等；④多維空間信息複合。利用二維影像複合成三維影像，有助於分析地物空間分布特徵；⑤多種空間信息複合。如影像數據與地圖...
2.8 複合次數分布 2.9 泊松-二項分布 2.10 Neyman-A分布 2.11 Polya-Aeppli分布 2.12 泊松-Pascal分布 第3章 極大似然估計 3.1 極大似然估計的定義 3.2 極大似然估計的性質 3.3 極大似然估計的有效性 3.4 特殊情形下...
這種層理的特徵是泥質沉積物主要分布在砂質波痕的波谷中，而在波脊上很薄或缺失，以致使泥質沉積物呈脈狀體分布在砂質沉積物之中。砂質沉積層內往往發育良好的波痕前積紋層（圖a）。脈狀層理是在波谷及部分波脊上含有泥質條紋的沙...
因為不同的電子和空穴具有不同的熱運動速度，一般來說，它們的複合幾率與它們的運動速度有關。這裡g表示不同熱運動速度的電子和空穴複合幾率的平均值。在非簡併半導體中，電子和空穴的運動速度遵守玻耳茲曼分布，因此，在一定溫度下，可以...
表面複合速度 表面複合速度（surface recombination velocity）是1998年公布的電氣工程名詞。公布時間 1998年，經全國科學技術名詞審定委員會審定發布。出處 《電氣工程名詞》第一版。
4．水動力一構造一地層複合油氣藏 該類油氣藏實例不多見。美國印第安盆地氣田上賓夕法尼亞亞系白雲岩產層中的氣藏，和前蘇聯巴拉哈內一薩本奇一拉馬內油藏可能是較為典型的三元複合油氣藏。前者氣藏的分布區僅在西南側和東側有面積較...
喬木類樹大根深，主根一般分布在深層，而花灌木苗小根淺，一般分布在20~30cm的表土層，二者在土壤利用的空間分布上沒有根本衝突，土壤得到充分利用。二是花灌木經營時間短，一般1~2年要起挖出售，圃地土壤要重新翻耕和施肥，對喬木的...
大面積的高寒草甸分布在中國青藏高原的東部及其周圍的高山，例如祁連山、天山和橫斷山，是這些山地的植被垂直帶譜中的組成部分。高寒草甸的下部與高寒灌叢呈複合分布，上部與高寒墊狀植被接壤。一般海拔3500～5000米。分布界線從北向南逐漸...
，則它是一個複合假設。又如，關於某事件機率P的假設，H₀：P=P₀——簡單假設，而 H₁：P≠P₀ ——複合假設；其中H₀：總體服從標準正態分布——簡單假設， H₁：總體服從常態分配——複合假設。簡單備擇假設 如果 ...
累積分布 累積分布函式（Cumulative Distribution Function）描述的是實數隨機變數X的機率分布情況。柯爾莫諾夫-斯米爾諾夫檢驗（Kolmogorov-Smirnov test）正是基於累計分布函式，以檢驗兩個經驗分布是否不同或一個經驗分布與另一個理想分布是否...
