若爾當矩陣(Jordan matrix)一種重要的具有特殊形式的矩陣。
基本介紹
- 中文名:若爾當矩陣
- 外文名:Jordan matrix
定義
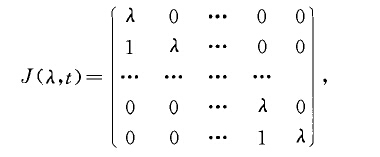
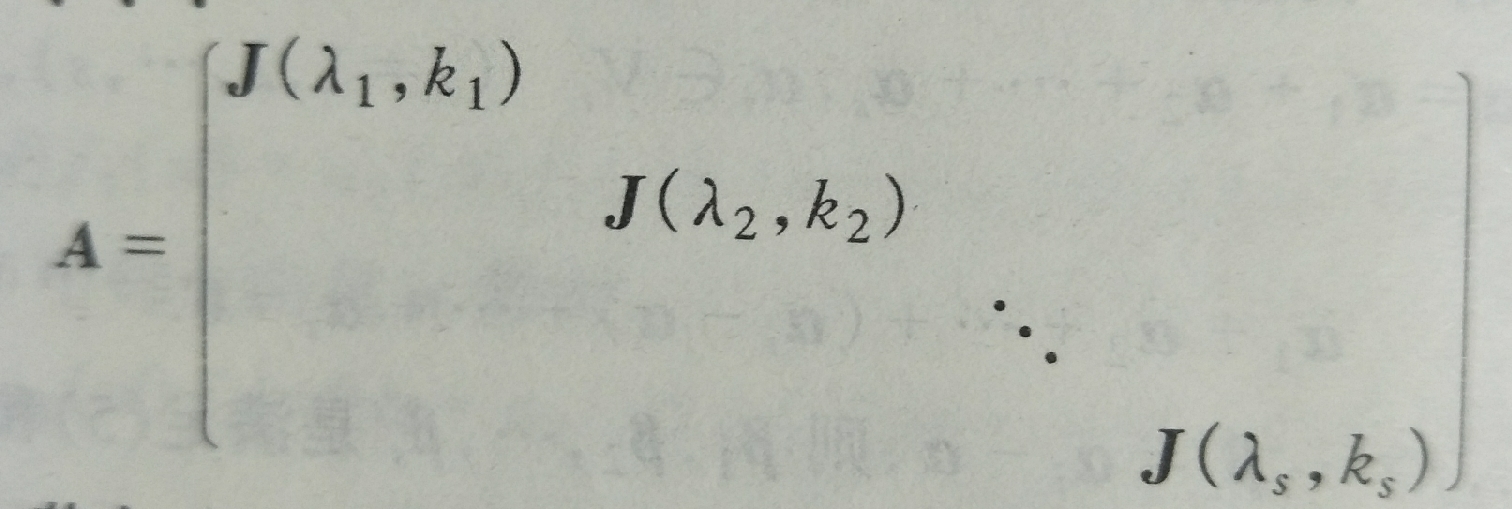
例題
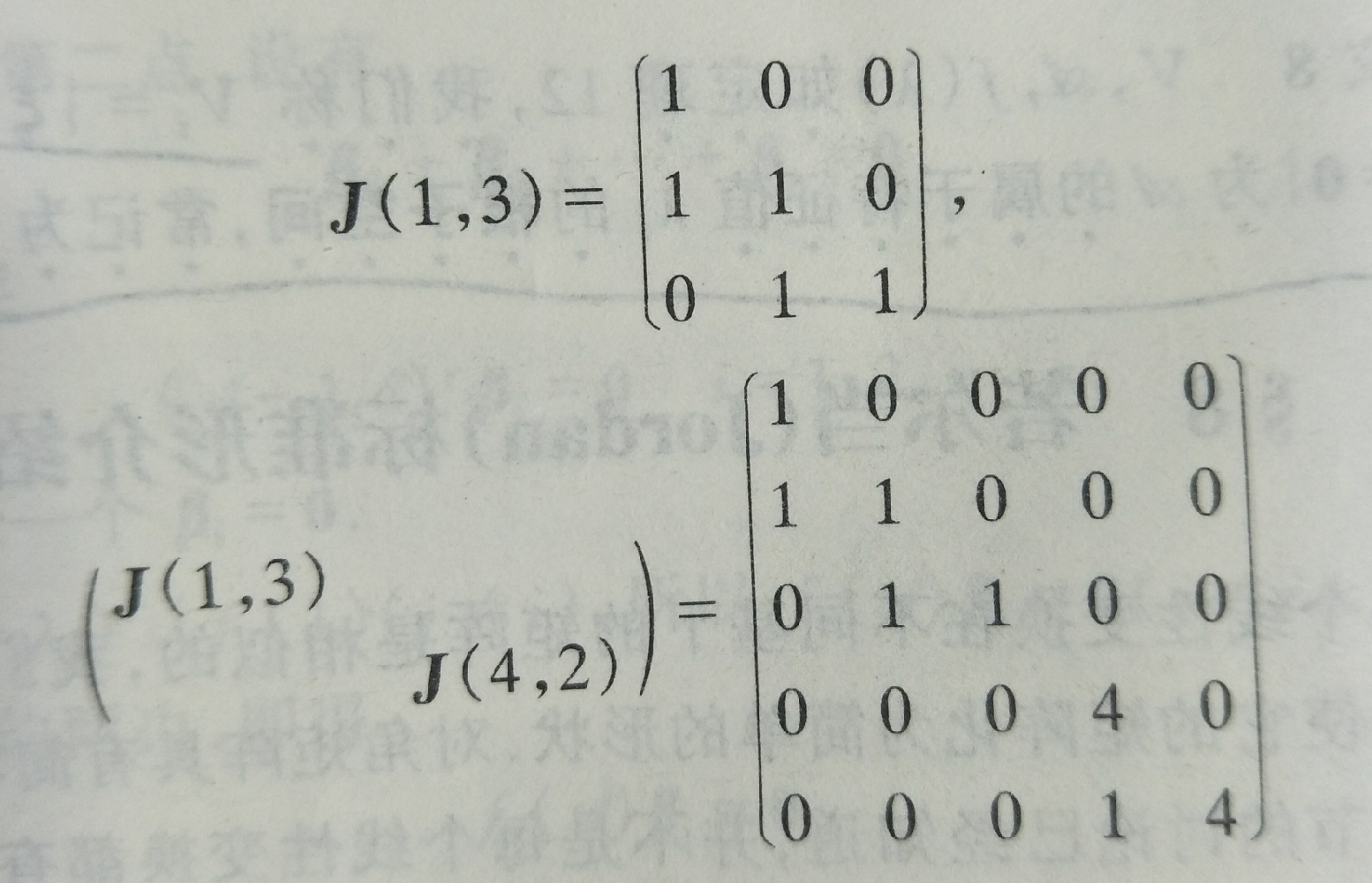
若爾當矩陣(Jordan matrix)一種重要的具有特殊形式的矩陣。

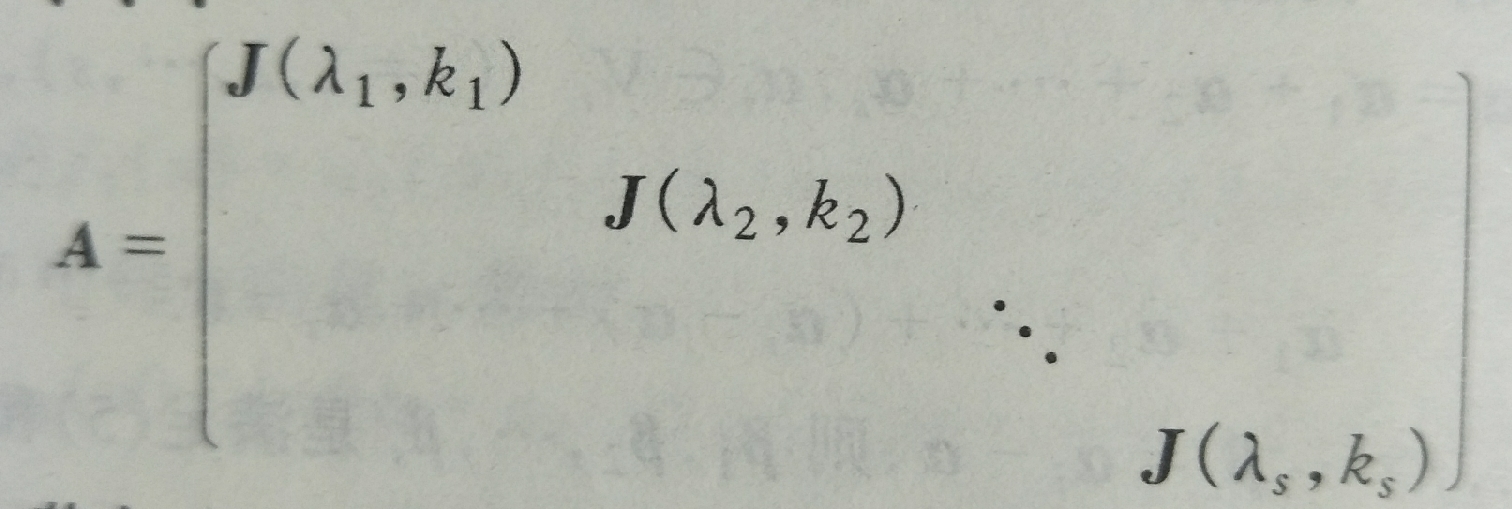
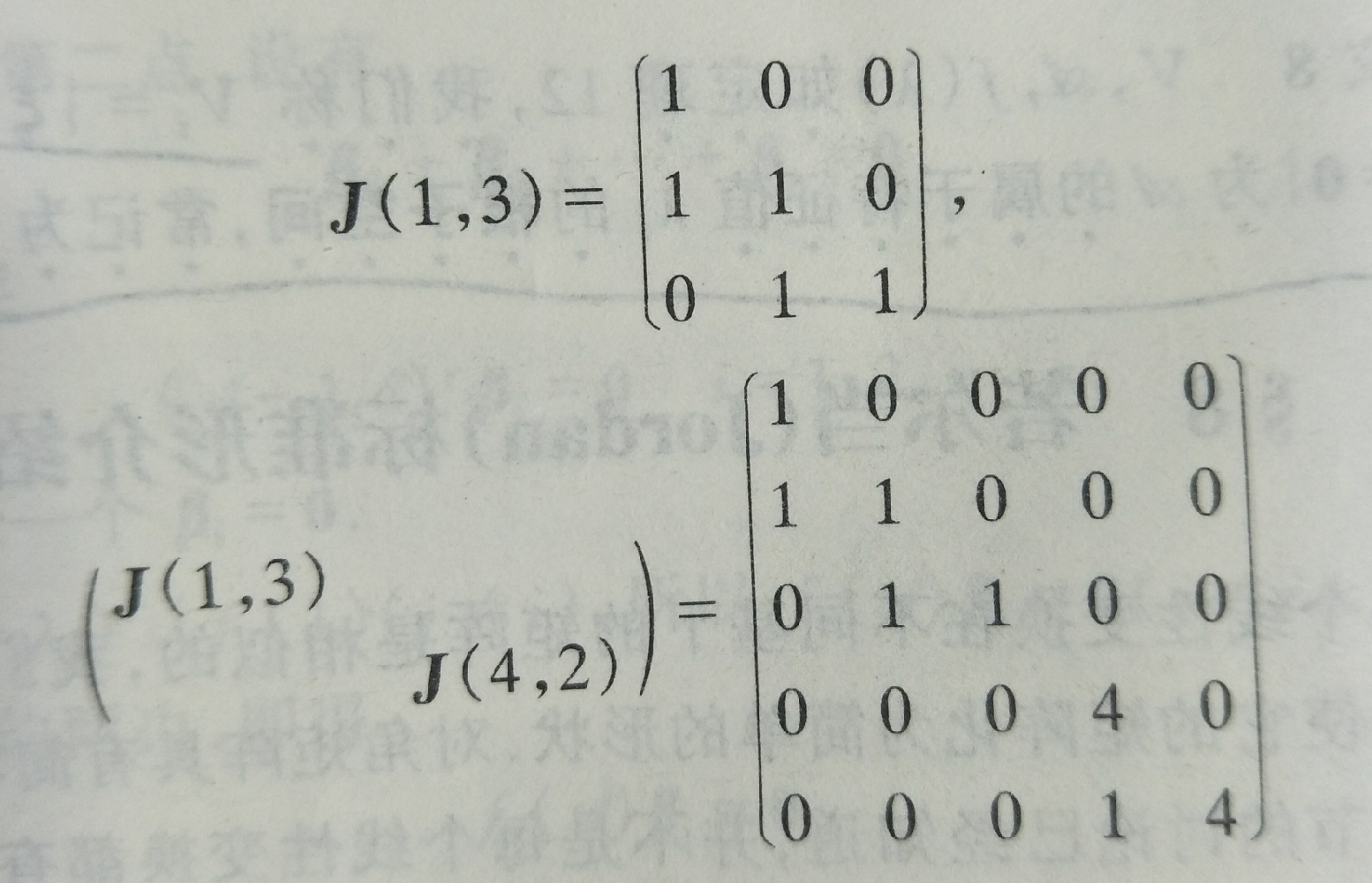
若爾當矩陣(Jordan matrix)一種重要的具有特殊形式的矩陣。定義若爾當矩陣(Jordan matrix)一種重要的具有特殊形式的矩陣。即形式為J(λ,t)的矩陣稱為一個若爾當塊,其中λ是複數,由若干個若爾當塊組...
這裡的“簡單”是指每小塊矩陣都具備一種很簡單的形狀:其中主對角線上都是同一個係數,而對角線上方一排全是1。形同以上 的矩陣稱為若爾當矩陣。而矩陣J中每一個這樣的小塊被稱為若爾當塊。線性代數中有如下的結果:對任意係數...
n×n自相關實數矩陣的若爾當代數如上。n×n自相關複數矩陣的若爾當代數如上。n×n自相關四元數矩陣的若爾當代數。如上。約旦代數由Rn與關係自由產生 其中右側使用Rn上的通常的內積來定義。這有時被稱為自旋因子或Clifford類型的若爾...
本教材根據(全日制、在職)工程碩士研究生的特點和培養創新型人才的要求,將矩陣論與數值分析的有關理論與方法按內容體系編寫.全書共6章,分別是矩陣運算與矩陣分解、線性空間與線性變換、矩陣的若爾當標準形與矩陣函式、方程與方程組的...
矩陣論與數值分析:理論及其工程套用》由邱啟榮編著,《全國工程碩士專業學位教育指導委員會推薦教材:矩陣論與數值分析:理論及其工程套用》共6章,它們是矩陣運算與矩陣分解、線性空間與線性變換、矩陣的若爾當標準形與矩陣函式、方程與方程組...
高斯-若爾當消元法(英語:Gauss-Jordan Elimination),或譯為高斯-約旦消元法,簡稱G-J消元法,是數學中的一個算法,是高斯消元法的另一個版本。它線上性代數中用來找出線性方程組的解,其方法與高斯消去法相同。唯一相異之處就...
第2章至第4章主要介紹λ矩陣與若爾當標準形、矩陣的分解、賦范線性空間與矩陣範數. 這些內容是矩陣理論研究、矩陣計算及套用中不可缺少的工具和手段. 以上4章內容均為1991年國家教育委員會工科研究生數學課程教學指導小組對“矩陣論”課...
《矩陣論引論》全面系統地介紹了與工程技術聯繫密切的矩陣理論及其套用,注重理論和套用的結合,具有工科教材的特點和方法。全書共6章,分別介紹了線性空間與線性變換、內積空間、矩陣的若爾當標準形及其分解、矩陣分析及套用、特徵值的估計...
λ矩陣與若爾當標準形 ………94 習題 2 ………94 第3章矩陣的分解 ………122 習題 3 ………122 第4章賦范線性空間與矩陣範數 ………156 習題 4(1)………156 習題 4(2)………165 習題 4(3)………179 第5章矩陣微積...
若爾當曲線定理,複雜分析所需的拓撲結果;若爾當正態形式和若爾當矩陣,線上性代數中有重要作用;在數學分析中,若爾當衡量是度量理論之前的區域度量;在組合理論中,若爾當 - 霍德定理組成系列是一個基本的結果。若爾當定理有限線性組...
《矩陣論千題習題詳解》是2015年清華大學出版社出版的圖書,作者是方保鎔。圖書目錄 第1章矩陣的幾何理論 習題1(1)習題1(2)習題1(3)習題1(4)習題1(5)第2章λ矩陣與若爾當標準形 習題2 第3章矩陣的分解 習題3 第4章賦...
利用相似矩陣和特徵方程的概念,證明矩陣可化為標準型,現稱為“若爾當標準型。若爾當的名著《論置換與代數方程》(Traité des substitutions et des équations algébriques)於1870年首版,在數學界產生了很大的影響,長期被作為群論中的...
本書是一部英文版的圖論專著,中文書名或可譯為《強正則圖與歐幾里得若爾當代數:非通常關係中的啟示》。本書的基本內容是研究在強正則圖的參數上尋找合適的容許性條件的問題,並且加入了在這個領域中作者自己的貢獻。由單位矩陣與強正則...
第3章矩陣的分解49 3.1若爾當(Jordan)型分解49 3.1.1λ矩陣及其性質49 3.1.2n階方陣的若爾當標準形54 3.1.3單純矩陣的譜分解61 3.2n階方陣的三角分解62 3.2.1矩陣的三角分解62 3.2.2三角分解的套用64 3.3埃爾米特...
方塊矩陣 的行列式是其 個特徵值的積, 但亦可經由Leibniz formula計算出來。可逆矩陣正好是那些行列式非零的矩陣.高斯-若爾當消元法非常重要,可以用來計算矩陣的行例式,秩,逆矩陣,並解決線性方程組。矩陣的跡是 矩陣的對角線元素...
特徵分解是將一個矩陣A寫成PDP的形式,其中P是一個可逆矩陣,D是對角矩陣。如果A的特徵分解存在,就稱它是可對角化的矩陣。不能對角化的矩陣,也有類似的分解方式。任意的矩陣A都可以寫成PJP的形式,其中的矩陣J是若爾當標準型。
若爾當利用相似矩陣和特徵方程的概念,證明了矩陣經過變換可相似於一個“標準型”,即所謂的若爾當標準型。在若爾當工作的基礎上,弗羅貝尼烏斯討論了契約矩陣與契約變換。弗羅貝尼烏斯關於矩陣理論的工作於1877年發表在《克雷爾雜誌》上。
專題2 λ矩陣與矩陣的相似標準形 2.1 問題的提出 2.2 λ矩陣及其基本性質 2.3 λ矩陣的等價及其標準形 2.4 λ矩陣等價標準形的唯一性 2.5 矩陣相似的條件 2.6 有理標準形 2.7 若爾當標準形 2.8 若爾當標準形的套用 2....
9.1 矩陣的相似對角化 9.1.1 矩陣可對角化的條件 9.1.2 求相似對角陣的方法 9.2 低階矩陣的若爾當標準形 9.2.1 例子 9.2.2 求低階方陣的若爾當標準形的一般方法 9.3 空間分解與若爾當標準形理論 9.3.1 極小多項式...
Marie ENNEMOND (1838-1922),數學家,若爾當標準型、若爾當矩陣、若爾當曲線定理、若爾當測度以及若爾當-赫爾德定理的發明者。Henri Léon LEBESGUE (1875-1941),數學家,勒貝格積分的創始者。Henri CHATELIER (1850-1936),化學家,...
7.1λ-矩陣 258 7.2λ-矩陣的等價不變數 265 7.3 特徵矩陣 275 7.4 若爾當標準形 284 複習與提高題7 293 第8章 二次型 295 8.1 二次型的矩陣表示與矩陣的契約 295 8.2 標準形 298 8.3 慣性定理 308 8.4 正定二...
9.1矩陣的相似對角化 9.1.1矩陣可對角化的條件 9.1.2求相似對角陣的方法 9.2低階矩陣的若爾當標準形 9.2.1例子 9.2.2求低階方陣的若爾當標準形的一般方法 9.3空間分解與若爾當標準形理論 9.3.1極小多項式 9.3.2誘導...
