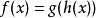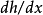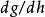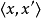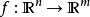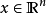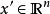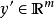基本介紹
- 中文名:自動微分
- 外文名:Automatic differentiation
- 又稱:演算式微分
- 本質:一個函式導數的方法
簡介,複合函式求導法則,前向式積累自動微分的由來與二元數,向量參數和函式,更高階微分,程式碼轉換,運算符重載,
簡介
自動微分使用這個事實:任何實作一個向量函式y=F(x)的電腦程式,一般而言,可以被分解成由基本指定運算所成的序列,而其中每一個都可以藉由查表而輕易地微分。這些計算某一特定項的 "基本偏微分" 是依照微積分中的複合函式求導法則來合併成某個 F 的微分資訊(如梯度、切線、雅可比矩陣等)。這個過程會產生確實(數值上準確)的導數。因為只在最基礎的層面做符號轉換,自動微分避免了複雜的符號運算的問題。
複合函式求導法則
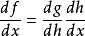
前向積累
前向積累式的自動微分是最容易理解和實作的。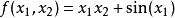 這個函式是可被電腦(或程式設計師) 解釋成一連串對變數
這個函式是可被電腦(或程式設計師) 解釋成一連串對變數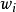 的運算。 前向積累式自動微分的工具則會增加相對應的作用於第二項上的運算。
的運算。 前向積累式自動微分的工具則會增加相對應的作用於第二項上的運算。
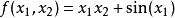
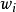
計算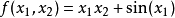 的導數需要初始化, 以區別是要對
的導數需要初始化, 以區別是要對 或
或 來求導數。 上述表格則以
來求導數。 上述表格則以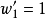 和
和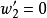 來初始化, 並且我們可以看到其結果
來初始化, 並且我們可以看到其結果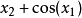 正是對
正是對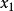 的導數。 注意,雖然表格列出了符號微分, 但以電腦的角度而言,電腦總是儲存數值。圖一則以圖形表明上述的敘述。
的導數。 注意,雖然表格列出了符號微分, 但以電腦的角度而言,電腦總是儲存數值。圖一則以圖形表明上述的敘述。 圖一
圖一
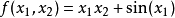


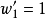
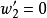
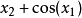
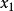
 圖一
圖一為了計算這個例子的導數,其分別為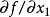 和
和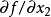 , 需要計算兩次,一次是以
, 需要計算兩次,一次是以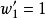 和
和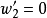 做初始值, 另一次則以
做初始值, 另一次則以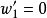 和
和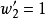 做為初始值。
做為初始值。
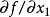
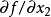
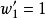
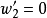
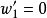
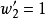
前向積累的計算複雜度則正比於原來程式的計算複雜度。
對於函式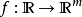 且
且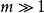 來說, 前向積累只要計算一次,優於需要計算m次的反向積累。
來說, 前向積累只要計算一次,優於需要計算m次的反向積累。
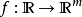
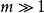
前向式積累自動微分的由來與二元數
前向式積累自動微分可藉由擴充實數中的代數並得到一個新的算術系統來達成。 每一個數都會新增另一數,用來表示一函式在這數上導數的數。 而每一個算術運算都被擴充於此新的代數。 這個擴充後的代數就是二元數的代數。
將每一個數

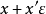
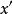


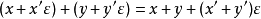
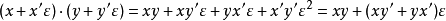
減法和除法則類似。
我們可以計算多項式。 如果 ,則
,則

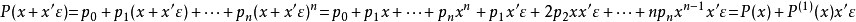
其中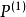 表示
表示 對第一個參數的導數。 而
對第一個參數的導數。 而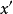 則稱作“種子”,可以任意選擇。
則稱作“種子”,可以任意選擇。
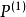

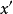


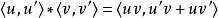
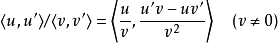
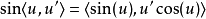
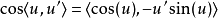
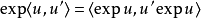
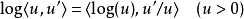
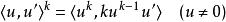
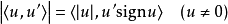
並且,一般而言,對於一個函式{\displaystyle g},我們會有

其中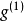 和
和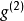 分別是
分別是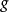 對其第一項和第二項的導數。
對其第一項和第二項的導數。
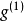
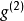
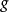
對一個二元算術運算作用於混合的參數時(數對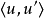 和實數
和實數 ), 實數會先被轉成
), 實數會先被轉成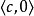 。 函式
。 函式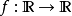 在
在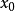 上的導數 則為以上述算術計算
上的導數 則為以上述算術計算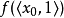 ,其結果為
,其結果為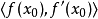 。
。
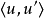

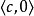
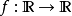
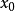
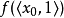
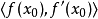
向量參數和函式
更高階微分
以上的算術可以被一般化,以用於二階及三階導數。 然而,此算術的規則將會迅速變得複雜。 其複雜度將與最高階導數階數成平化。 取而代之的是使用限縮泰勒級數。 這是可行的,因為函式的泰勒級數中的通項為己知係數和函式導數的乘積。 使用自動微分來計算黑塞矩陣在某些最佳化已被證明是可行的。
前向式積累是由對程式的非標準化轉譯程式來實作。 即將實數替換成二元數,常數則換成有第二項為零係數的二元數。 而數值上基本運算則被換成二元數的運算。 非標準化轉譯程式一般使用兩者策略之一:程式碼轉換和運算符重載。
程式碼轉換
一個函式的程式碼會被自動產生的程式碼所替換, 新生成用來計算導數的程式碼則會插入原程式碼中。
程式碼轉換可實作在所有的程式語言上,且它對編譯器而言,是容易最佳化的。 然而,實作自動微分的工具則是比較困難的。
運算符重載
如果所使用的程式語言支持,運算符重載是個可行的方法。 實數的物件跟基本數學運算必須重載以滿足上述 augmented 算術。 這不須要改變要被微分的函式的程式碼。
運算符重載對前向積累是容易實作的,並且可能對反向積累亦如此。 然而,與前向積累相比,現有的編譯器在最佳化程式碼方面則是較為落後。