能量泛函(energy functional)映射的微分的模長平方的積分。
基本介紹
- 中文名:能量泛函
- 外文名:nergy functional

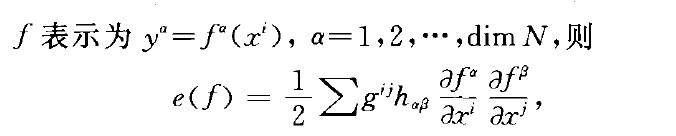
能量泛函(energy functional)映射的微分的模長平方的積分。

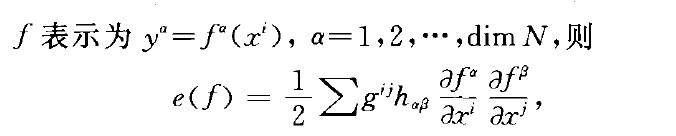
霍恩伯格-科恩能量泛函 霍恩伯格-科恩能量泛函(Hohenberg-Kohn energy functional)是2019年發布的物理學名詞。公布時間 2019年經全國科學技術名詞審定委員會審定發布。出處 《物理學名詞》第三版。
更一般的我們會遇到非線性的運算元。最簡單的例子就是各種函式空間上不同的能量泛函。非線性的運算元在微分幾何和微分方程理論中都扮演重要的角色,比如極小曲面就是能量泛函的極小點。特點和內容 泛函分析的特點是它不但把古典分析的基本概念...
全書共10章:第1章為能量原理概述;第二-四和六-七章按學科分類依次介紹能量原理的基本理論,學科內容包括結構力學、彈性力學、薄板理論和厚板理論;第五和八-十章介紹學科進展,包括能量原理的變換格式、互伴自伴運算元示例與能量泛函通式...
能量泛函是映射的微分的模長平方的積分。設M和N為黎曼流形,f:M→N為光滑映射,f的能量定義為:式中df為f的微分,*1是M的體積元,E稱為能量泛函,稱為能量密度。第一變分公式 第一變分公式是計算能量泛函的一階變分公式。若f:...
設M和N為黎曼流形,f:M→N為光滑映射,若f的張力場τ(f)恆為零,則稱f為調和映射.由第一變分公式可知:調和映射是能量泛函的臨界點;反之,若f是能量泛函在每一個緊緻區域DM上關於保持邊界D不動的變分的臨界點,則f必是調和...
中,使泛函取駐值(即一階變分 )的 為本問題的精確解。馬爾克夫變分原理將上式描述的剛塑性材料的邊值問題歸結為能量泛函對位移速度場 的極值問題,避開了偏微分方程的求解困難,一旦求得速度場的精確解後,就可以利用上式求出應變速率場...
若uEL;(M,N)且對任何的wEL;(M,N),u}ay=w}*都成立E(u)鎮E(w),則稱u為能量極小映射.此時,u是能量泛函E的形式上的歐拉一拉格朗日方程:}u)=。的弱解,u不一定是光滑的;但是,若在xEM的一個鄰域內u是連續的,則在該...
由於知道該方程的能量泛函即K-能量,我們計畫用Trudinger-Wang在研究仿射Plateau問題時採用的變分方法來研究解的存在性。我們近期對這兩個方面的研究都已經有一些重要的進展,我們將在此基礎上做更深入的研究。結題摘要 本項目主要圍繞...
1964年,Hohenberg和Kohn以這個模型為基礎,同時打破其能量泛函形式的束縛,創立了嚴格的密度泛函理論。基本介紹 1926年奧地利科學家薛丁格提出了Schrdinger方程,薛丁格方程是量子力學中的一個基本方程和基本假定,其正確性只能通過實驗來檢驗。
探討具有指定曲率的曲面與其相對應的面積泛函的臨界點之間的關係,以及Carnot群上的極小曲面的性質,如存在性、正則性等;深入研究度量空間之間的Sobolev映射的性質,重點研究介於兩個Carnot群的Sobolev映射所對應的能量泛函之極小的正則性。
● 江蘇省高校自然科學面上項目,面積泛函的近似能量泛函構造及隱式極小曲面,2018.09.01-2020.08.31,主持,在研 ● 國家自然科學天元項目,基於極小曲面的幾何造型理論及套用,2016.01.01-2016.12.31,主持,已結題 學術論文 ●...
復射影空間、toric Kaehler流形、Hermitian對稱空間或一般的廣義旗流形中的拉格朗日子流形的構造、刻畫及哈密頓變分問題,Oh猜想,Austere子流形、等參超曲面和特殊拉格朗日子流形的關係以及歐氏空間中異向表面能量泛函的幾何。
變分方法是非線性泛函分析的主要工具之一,是現代數學的重要研究領域,在非線性微分方程等領域有非常廣泛和深刻的套用。但是,當微分方程具有衰減位勢時,微分方程所對應的能量泛函在通常的Sobolev空間沒有定義,這時,變分方法便不能施展它...
本項目中,我們在余維1的情形下丟棄周期性條件,這時變分結構也會受到影響,因為此時相應的能量泛函的最小值是無窮,從而沒有最小能量構型(或最小解)。這種情形最簡單的例子是柱面上非正合的保面積單調扭轉映射,對應的物理模型是受...
在典則度量和穩定性研究方面,我們得到了復約化李群緊化空間上各種典則度量存在性和各種能量泛函的關係。對於環流形的相對K穩定性和Chow穩定性,我們也做了約化並確定了很多3維Fano環流形的穩定性。在Monge-Ampere型方程的研究方面,...
在密度泛函理論的庫普曼斯定理中,誤差的主要來源是交換相關能量泛函的不準確性,這點與哈特里-福克近似不同,因此在改進計算結果上有較大的提高空間。哈特里-福克方程 哈特里-福克方程(英語:Hartree–Fock equation),又稱為HF方程...
主要研究思路是將變分法、偏微分方程和傳統圖像處理技術結合起來,提出一些新的變分模型,並套用添加輔助變數法、對偶方法、運算元分裂方法等設計快速高效的數值算法,理論方面研究對應能量泛函解的存在唯一性,對應Euler-Lagrange方程(組)或...
再次,通過能量泛函與Z2指標研究了對稱動力系統的全局吸引子的多重平衡點的存在性,揭示了吸引子具有無窮維分形維數的特性,反映了該吸引子幾何結構的複雜性。最後,我們對具有動力學邊界條件的二相流模型進行了研究,證明了其吸引子的...
有限元線法(FEMoL:FiniteElementMethodofLines)是一種新型的以常微分方程求解器為支撐軟體的半解析數值方法·在這種方法中,首先利用有限元技術,藉助於能量泛函的變分,將控制偏微分方程半離散化為用結線函式表示的常微分方程組,然後選用...
2n維歐氏空間中任意緊星形超曲面上總存在至少2個閉特徵(退化情形)。擬採用的方法有:創建莫爾斯concavity的疊代理論;發展數論中的相關理論來研究疊代中的無理旋轉角;建立能量泛函水平集的同調理論來聯繫流形的整體性質與局部性質等等。
7.2.1 哈密頓系統和能量泛函 176 7.2.2 Fenchel 變換和對偶原理 178 7.2.3 kT-周期解的存在性 180 7.2.4 次調和解的存在性 186 7.3 二階差分系統的反周期解 189 7.3.1 序列空間和對偶泛函 190 7.3.2 反周期解的...
其基本思想是將複雜的多電子體系先簡化成沒有相互作用的電子在有效勢場中運動,而將電子相互作用歸入交換關聯的泛函中。Kohn和沙姆(Sham)提出了實用的能量泛函表達形式,因而在計算精度和時間之間達到了較好的平衡,在物理,化學,生物等...
