基本介紹
- 中文名:算術關係
- 外文名:arithmetical relation
- 所屬學科:數學
- 所屬問題:數理邏輯(遞歸論)
- 相關概念:遞歸關係,量詞,算術性等
- 提出者:克林,莫斯托夫斯基
基本介紹


相關性質與概念
相對算術關係










算術性







算術表示定理







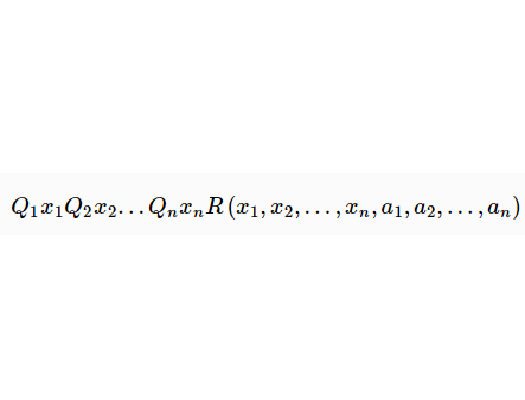


























算術關係(arithmetical relation)是遞歸關係的推廣,是可以通過對遞歸關係添加有窮個量詞定義的關係,即可以表示Q1x1Q2x2…QnxnR(x1,x2,…,xn,a1,a2,…,an)形的關係,其中R為...
相對算術關係是高等數學中的概念。 [1] 相對算術關係(relativized arithmetical rela -tion)算術關係概念的相對化.對自然數集A和關係R,若R可表示成(G2.za ) (R2.z'2 ) ''.. (G2 .z' ) S (.z, ,a.z...,a az,....
數學如此發展,算術已不再是數學的一個分支,我們通常提到的算術,只是作為國小里的一個教學科目,目的是使學生理解和掌握有關數量關係和空間形式的最基礎的知識,能夠正確、迅速地進行整數、小數、分數的四則運算,初步了解現代數學中的...
的算術平方根;零的平方根也叫做零的算術平方根,因此零的算術平方根仍舊為零。各部分的關係 乘法是加法的簡便運算,除法是減法的簡便運算。減法與加法互為逆運算,除法與乘法互為逆運算。加數+加數=和;被減數-減數=差;一個加數=和...
關係符號(relational symbols)是常用的數學符號之一,指在算術中表示兩個數、兩個式子或數與式之間數量關係的符號,算術中常用的關係符號有兩類:1.表示相等與不等關係的符號,如等號、不等號、近似等號等;2.表示大小關係的符號,如...
8.關係符號:=; ≠;>;9.結合符號:( );[ ];{ };10.省略符號:sin;cos;f(x)。舉例 在下面的數中填上合適的算術符號使等式成立。4 4 4 4=0 4 4 4 4=1 4 4 4 4=2 4 4 4 4=7 4 4 4 4=8 4 4 ...
第六章分數與小數之關係 1.小數化分數 2.分數化小數 3.循環小數 新教育高等國小算術教科書第四冊 第七章名分數計算法 1.名分數化法 2.名分數四則 3.經度與時間之關係 4.溫度之計算 第八章百分法 1.百分之意義及記法...
《子群的正規性條件和算術性質與群結構的關係》是依託中山大學,由王燕鳴擔任項目負責人的面上項目。中文摘要 子群的正規性條件和一些基本量的算術性質是研究有限群結構的重要問題。我們擬研究子群的不同類型的正規性或交換性條件,通過對...
教學生同時用算術和代數的方法解決問題有以下三個益處:(1)通過對數量關係的算術和代數的表示,幫助學生對數量關係的深度理解;(2)引導學生髮現算術方法和代數方法之間的相似和差異,以便理解更一般的代數方法的威力;(3)發展學生的...
算術集(arithmetical set)一元算術關係的自然數集.指能表示成形如x: W W z.Y2, ...RnynS Cy,yn , . 的自然數集,其中W ,z,…,Q。為一階量詞」或fl,S為n十1元遞歸謂詞一集合A為算術集,若且唯若存在自然數n,使...
在國小算術教學中明確地提出掌握知識、發展智力、培養能力以及進行思想教育的任務。1978年中華人民共和國教育部制訂的《全日制十年制學校國小數學教學大綱(試行草案)》中規定:國小數學教學的目的是:使學生理解和掌握數量關係和空間形式的最...
這種對應關係是由用戶來定義的,不過一般通用編碼器會有約定俗成的含義。圖1是一個計算器鍵盤上的數字和字元被轉換成二進制代碼的編碼器說明圖。通過按壓每個鍵盤,分別產生對應的高電平輸入.從而在輸出編碼端產生對應的二進制代碼。7....
關係運算符的值只能是0或1。關係運算符的值為真時,結果值都為1。關係運算符的值為假時,結果值都為0。注意事項 (1)前4種關係運算符的優先權別相同,後兩種也相同。前四種高於後兩種。(2)關係運算符的優先權低於算術運算符。
少”來表示的靜態的數量關係。研究發現,變化型問題,無論是數量的增加還是減少都相對較容易;比較型問題難度最大,其難度主要取決於未知量的位置:結果項未知的問題比中間項未知的問題容易,初始項未知的問題最難。研究指出這一分型不夠...
數學上,二元關係用於討論兩個數學對象的聯繫。諸如算術中的「大於」及「等於」,幾何學中的"相似",或集合論中的"為...之元素"或"為...之子集"。二元關係有時會簡稱關係,但一般而言關係不必是二元的。定義 集合X與集合Y上的...
相對解析分層(relativized analytical bierarchy)是解析分層概念的相對化。即對相對算術關係依量詞複雜性進行的遞歸論分層。概念 相對解析分層(relativized analytical bierarchy)是解析分層概念的相對化。即對相對算術關係依量詞複雜性進行的遞歸...
皮亞諾公理是義大利皮亞諾所構造的算術公理系統中的公理。1889年,在數學家戴德金工作的基礎上,皮亞諾在《用一種新方法陳述的算術原理》一書中提出了一個算術公理系統,這個公理系統有九條公理,其中四條是關於“相等”的,五條是...
根據除法的意義,除法是已知兩個因數的積與其中一個因數,求另一個因數的運算。利用除法與乘法的互逆關係可知,如果除數為0,則:① 當被除數不為0(例如3÷0),由於“任何數乘0都等於0,而不可能等於不是0的數(例如3)”,...
特別注意,所有的邏輯運算都是按位進行的,位與位之間沒有任何聯繫,即不存在算術運算過程中的進位或借位關係。下面舉例說明。【例1.1】 如兩變數的取值 X=00FFH,Y=5555H 求Z1=X∧Y;Z2=X∨Y;Z3=;Z4=XY的值。解:X=...
數學速算法是指利用數與數之間的特殊關係進行較快的加減乘除運算的計算方法。數學速算法分為金華速算、魏德武速算、史豐收速算以及古人創造的“袖裡吞金”四大類速算方法。分類 金華速算 金華全腦速算的運算原理是通過雙手的活動來刺激大腦...
透過數論也可以建立實數和有理數之間的關係,並且用有理數來逼近實數(丟番圖逼近)。按研究方法來看,數論大致可分為初等數論和高等數論。初等數論是用初等方法研究的數論,它的研究方法本質上說,就是利用整數環的整除性質,主要包括...
計算的定義有許多種使用方式,有相當精確的定義,例如使用各種算法進行的“算術”,也有較為抽象的定義,例如在一場競爭中“策略的計算”或是“計算”兩人之間關係的成功機率。將7乘以8(7x8)就是一種簡單的算術。數學中的計算有加,...
在其中我們只關心各種關係及其性質,而對於“數本身是什麼”這樣的問題並不關心。常見的代數結構類型有群、環、域、模、線性空間等。介紹 在古代,當算術里積累了大量的,關於各種數量問題的解法後,為了尋求有系統的、更普遍的方法,以...
關係 乘法是加法的簡便運算,除法是減法的簡便運算。減法是加法的逆運算,除法是乘法的逆運算。加數+加數=和 被減數-減數=差 一個加數=和-另一個加數 減數=被減數-差 被減數=差+減數 因數×因數=積 一個因數=積÷另一個因數 被...
歐拉在1748年發現了有名的關係式,並且是他在《微分公式》(1777年)一文中第一次用i來表示-1的平方根,首創了用符號i作為虛數的單位。“虛數”實際上不是想像出來的,而它是確實存在的。挪威的測量學家韋塞爾(1745年~1818年)在...
