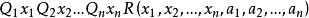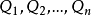算術表示定理

算術表示定理是美籍奧地利數學家哥德(Gode1,K.)於1931年證明的.。算術表示定理是指算術關係可用一階算術公式表示的定理。

基本介紹

• 中文名：算術表示定理
• 外文名：arithmetical representationtheorem
• 適用範圍：數理科學

簡介

算術表示定理是指算術關係可用一階算術公式表示的定理。

它指出：一關係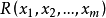為算術關係（即 R 在算術分層中），若且唯若 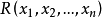在一階算術中可定義，即存在一階算術中的公式 ，使得對任何自然數 為真，若且唯若 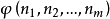在一階算術中為真。

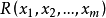
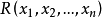
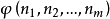
這也是“算術分層”與“算術關係”一詞的來源。算術表示定理是美籍奧地利數學家哥德爾(Godel,K.)於 1931 年證明的。

算術關係

算術關係是可以通過對遞歸關係添加有窮個量詞定義的關係。

算術關係可以表示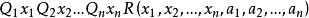形的關係，其中R為遞歸關係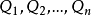，為一階量詞∃或ᗄ。等價地，算術關係亦是可以從遞歸關係出發，經有限次否定與射影運算得到的關係。

算術關係的定義是由美國邏輯學家、數學家克林(S.C.Kleene)與波蘭數學家莫斯托夫斯基(A.Mostowski)給出的。從可判定(或可計算)的角度上說，遞歸關係具有最小的複雜性，但遞歸關係對(不受限)量詞不封閉，而算術關係類則為遞歸關係類對量詞封閉的最小擴張，因此算術關係的概念可看做遞歸關係概念的推廣，實際上，任何算術關係也恰為一階算術可定義關係，這也是“算術”一詞的來源。