設(a0,a1,...,ar,...)是一個序列,把該序列中的ar和它前面的幾個ai(0≤i<r)關聯起來的方程稱做一個遞歸關係。如關係式:ar=3ar-1 (r≥1)和錯排數:Dn=(n-1)(Dn-1+Dn-2
) (n=3,4,...),都是遞歸關係。
基本介紹
- 中文名:遞歸關係
- 外文名:recursive relation
- 學科:數學
- 套用領域:,數學,計算機科學
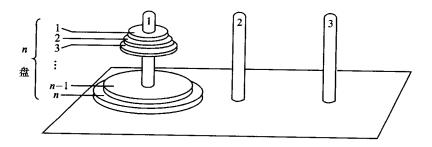
- 遞歸關係模型:斐波那契序列,河內塔
定義
遞歸關係模型
斐波那契序列



















河內塔


套用
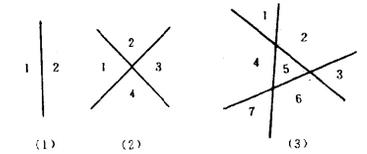

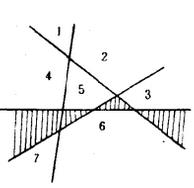

設(a0,a1,...,ar,...)是一個序列,把該序列中的ar和它前面的幾個ai(0≤i<r)關聯起來的方程稱做一個遞歸關係。如關係式:ar=3ar-1 (r≥1)和錯排數:Dn=(n-1)(Dn-1+Dn-2
) (n=3,4,...),都是遞歸關係。

























設(a0,a1,...,ar,...)是一個序列,把該序列中的ar和它前面的幾個ai(0≤i<r)關聯起來的方程稱做一個遞歸關係。如關係式:ar=3ar-1 (r≥1)和錯排數:Dn=(n-1)(Dn-1+Dn...
線性遞歸關係 線性遞歸關係(linear recurrence)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
所謂解一個遞推關係式,也就是求其解析解,即關於n的非遞歸函式。常係數線性齊次遞推關係式 線性字眼的意思是序列的每一項目是被定義為前一項的一種線性函式。係數和常數可能視n而定,甚至是非線性地。一種特別的情況是當係數並不...
在數學和計算機科學中,遞歸指由一種(或多種)簡單的基本情況定義的一類對象或方法,並規定其他所有情況都能被還原為其基本情況。遞推公式 如果數列{an}的第n項與它前一項或幾項的關係可以用一個式子來表示,那么這個公式叫做這個數列...
所謂語言的遞歸性,是指語言結構層次和言語生成中相同結構成分的重複或相套。反覆地使用構成句法關係的有限的幾種句法規則,不斷地進行同功能替換,以構成複雜的短語或句子。解析 遞歸性是語言的根本性質之一, 語言的遞歸性賦予語言無限的...
遞歸序數(recursive ordinal)是一種可構造序數。α為遞歸序數是指存在(某個自然數集上的)遞歸關係R,使得R為良序,並且R給出良序與α同構。概念 遞歸序數(recursive ordinal)是一種可構造序數。α為遞歸序數是指存在(某個自然數集上的...
算術關係(arithmetical relation)是遞歸關係的推廣,是可以通過對遞歸關係添加有窮個量詞定義的關係,即可以表示Q₁x₁Q₂x₂…QₙxₙR(x₁,x₂,…,xₙ,a₁,a₂,…,aₙ)形的關係,其中R為遞歸關係,Q...
遞歸語言是在下列運算下是閉合的。就是說,如果L和P是兩個遞歸語言,則下列語言也是遞歸的:L的Kleene星號:L的非刪除(non-erasing)同態:φ(L)L和P的串接:並集:交集:L的補集:差集:圖靈可判定語言與圖靈可識別語言的關係 注意...
交叉遞歸圖比較兩個系統相似狀態的出現。它們可以用來分析兩個不同系統之間動力學演化的相似性,在兩個系統中尋找相似的匹配模式,或者用來研究兩個時間尺度不同的相似系統的時間關係(Marwan&Kurths 2005)。聯合遞歸圖是所考慮子系統的...
利用遞推公式和遞推關係導出的遞歸數列進行了系統地歸納分類,作為專篇進行探索。首先對遞歸數列的常見形式按題型進行分類,對每一種題型進行專節探討,以求得各種 題型的解題思路、方法和技巧。其次,對難度較大的遞歸數列的通項的求法...
2幾種非常規遞歸形式(055)2.1分式遞歸(055)2.2遞歸方程組(065)2.3多維遞歸(076)2.4遞歸不等式(104)習題2(122)習題2解答(126)3遞歸數列項的性質研究(144)3.1通項法(144)3.2直接利用遞歸關係法(153)3.3...
當遞歸神經網路的每個父節點都僅與一個子節點連線時,其結構等價於全連線的循環神經網路。遞歸神經網路可以引入門控機制(gated mechanism)以學習長距離依賴。遞歸神經網路具有可變的拓撲結構且權重共享,被用於包含結構關係的機器學習任務,...
亦稱遞歸列。由前面的項能推出後面的項的數列。指對所有n>p,滿足形如aₙ=f(a,a,…,a)的關係式的序列{aₙ},其中f為某個函式。p是某個固定的正整數,a₁,a₂,…,aₚ為已知數。p稱為這個遞推列的階數.上述...
recursive,英語單詞,主要用作形容詞,作形容詞時譯為“[數] 遞歸的;循環的”。短語搭配 recursive relation[數] 遞歸關係 ; 翻譯 recursive computation[數] 遞歸計算 ; 遞歸計算英語 ; 遞歸計算 recursive procedure[計] 遞歸過程 ...
recurrence relation遞迴關係式 ; 遞推關係 ;[數]遞歸關係 relation algebra[數]關係代數 congruence relation[數]同餘關係 Poor relation稍遜一籌 ; 無名小卒 indifference relation無差異關係 ; 無差異關聯 ; 無差異瓜葛 blood relation...
這也是“算術分層”與“算術關係”一詞的來源。算術表示定理是美籍奧地利數學家哥德爾(Godel,K.)於 1931 年證明的。算術關係 算術關係是可以通過對遞歸關係添加有窮個量詞定義的關係。算術關係可以表示 形的關係,其中R為遞歸關係,為一...
之間的關係可以用一個公式表示,這個公式就叫做這個數列的通項公式。數列中數的總數為數列的項數。特別地,數列可以看成以正整數集 (或它的有限子集 )為定義域的函式 . (需要注意的是,一些題目中可能會定義 )如果可以用一個公式...
1. }p為部分遞歸函式,若且唯若滬之圖G 卯為re集.2. f為遞歸函式,若且唯若其圖G (.f)為遞歸集.另一方面,一個部分函式獷之圖為遞歸,當且僅存在遞歸關係R,使}p(x)=f}yR(x}y).若取We筍。,則抓x)=}s(xEWe,)...
的關係式。此外,以下的條件也可以被驗證是與之等價的:純數數列 {cₙ}ₙ滿足c₀≠0,並且 純數數列 {cₙ}ₙ滿足c₀≠0,並且 其中 對所有的n= 0, 1, 2, ...,遞歸公式 假設 其中後一個等式是在以x為不定元的...
遞推算法是一種簡單的算法,即通過已知條件,利用特定關係得出中間推論,直至得到結果的算法。遞推算法分為順推和逆推兩種。概念基本思想 給定一個數的序列H0,H1,…,Hn,…若存在整數n0,使當n>n0時,可以用等號(或大於號、小於號)...
*8.5 遞歸關係及其解法 174 8.5.1 遞歸關係的定義 174 8.5.2 逆向代換法 177 8.5.3 常係數齊次線性遞歸關係 177 8.5.4 常係數非齊次線性遞歸關係 179 本章小結 180 習題八 180 第五篇 代數系統 第9章 代數系統 184 9...
記號系統,從一個自然數集D、到某個序數前節的映射二、,一個記號系統S,映射二。要滿足以下三個條件:為遞歸的,則稱S為遞歸相關的;若對任何可構造序數a,S中都有a的記號,則稱S為極大的;若對任何記號系統S},都存在部分遞歸函式...
4.2.4關係201 4.3實體-關係圖204 4.3.1E-R模型的不同版本205 4.3.2數據建模產品中E-R模型的變化205 4.3.3弱實體207 4.3.4ID依賴實體207 4.3.5非標識符依賴的弱實體209 4.3.6子類實體212 4.3.7遞歸關係213 4.4...
非邏輯符號用來表示論域上的斷言(關係)、函式及常數。以前標準上會對所有不同的用途使用相同的無限集的非邏輯符號,而最近則會根據套用的不同而使用不同的非邏輯符號。因此變得需要列舉出使用於一特定套用中的所有非邏輯符號。其選擇是...
第4章 遞歸 63 4.1 遞歸和遞歸算法 63 4.1.1 遞歸的概念 63 4.1.2 遞歸算法示例 64 4.2 歸納證明 66 4.3 遞推關係 67 4.4 實現遞歸 67 4.4.1 函式調用和系統棧 68 4.4.2 遞歸函式的...
|__||___|主謂關係 |__||___|述賓關係 |___||___|偏正關係 語法的層次性與語法的遞歸性密切相關。系統性 語法是一個嚴密的立體的開放的系統網路。所謂“嚴密”,是指系統的內部是相互制約的,要受到一定的規則的支配,不是...
數學子領域數值分析中的德卡斯特里奧算法(De Casteljau's algorithm),以發明者保爾·德·卡斯特里奧命名,是計算伯恩斯坦形式的多項式或貝濟埃曲線的遞歸方法。雖然對於大部分的體系結構,該算法和直接方法相比較慢,但它在數值上更為...
