基本介紹
- 中文名：等比差數列
- 外文名：𝗣𝗿𝗼𝗽𝗼𝗿𝘁𝗶𝗼𝗻𝗮𝗹 𝗱𝗶𝗳𝗳𝗲𝗿𝗲𝗻𝗰𝗲 𝘀𝗲𝗾𝘂𝗲𝗻𝗰𝗲
- 所屬學科：數學
一.比等差數列,定義,通項公式,二.差等比數列,定義,通項公式,
相關詞條
- 等比差數列
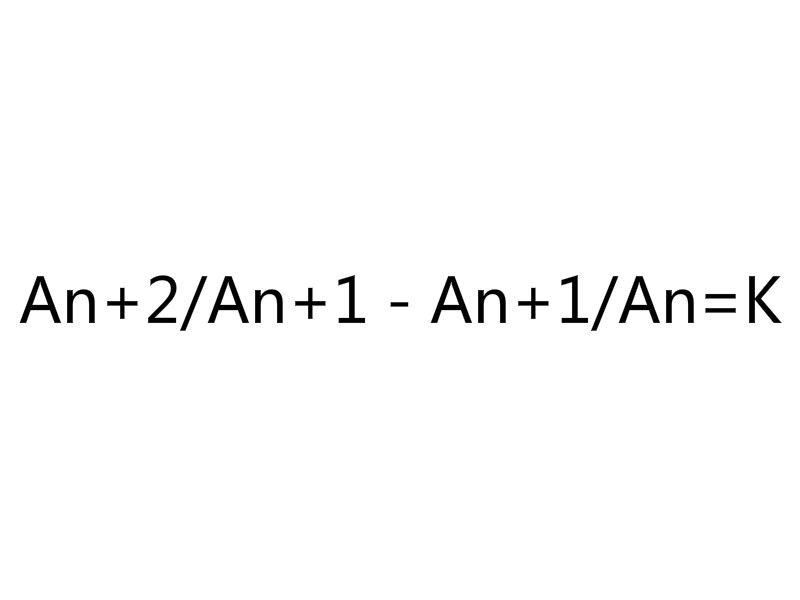
等比差數列，數學名詞。若數列滿足𝗮𝗻+𝟮/𝗮𝗻+𝟭-𝗮𝗻+𝟭/𝗮𝗻=𝗱;或𝗮𝗻+𝟮-𝗮𝗻+𝟭/𝗮𝗻+𝟭-𝗮𝗻=𝗾(𝗱,𝗾均為常數且𝗾≠𝟭),的數列統稱為等比差數列.(其中𝗱為公比差，𝗾為公差比)一.比等差數列定義若數列滿...
- 數列公式
高階等差數列 r階差等比數列的定義 通過對某一數列套用逐差法，使得若干階差後得到一等比數列。該數列又稱為高階差等比數列。定義 若一數列套用逐差法運算時，其前r階差不是等比數列，而r+1階差時是等比數列，則稱該數列為r階差等比數列 。通項公式：設數列(1)為r階差等比數列，其各階差首項分別為d1...
- 基本數列
1、常數列 常數列指的是由各個基本的數值組成，如：2、2、2、2、2、2。2、等差數列 等差數列指的是數列的相鄰數值差值是一個常數，如1、3、5、7、9，其公差為2。3、等比數列 等比數列指的是數列相鄰數值的比值是一個常數，如1、3、9、27、81，其公比為3。4、奇數數列 奇數數列指的是數列均由相鄰的...
- 差比數列
差比數列 差比數列，高等數學術語。一、定義 {cn}，cn=an·bn，其中{an}為等差數列，{bn}為等比數列,那么這個數列就叫做差比數列.由差比數列的定義可知，等差數列即當bn公比為1時差比數列的特殊形式，等比數列即當an公差為0時差比數列的特殊形式.二、前n項和公式 ...
- 數列的通項與遞推公式
等差數列的遞推公式：（d為公差）等比數列的遞推公式：（q為公比）遞推公式概念 數列中的每一個數都叫做這個數列的項。排在第一位的數稱為這個數列的第1項（通常也叫做首項），排在第二位的數稱為這個數列的第2項……排在第n位的數稱為這個數列的第n項。所以，數列的一般形式可以寫成a1，a2，a3，…，...
- 等比數列
等比數列是指從第二項起，每一項與它的前一項的比值等於同一個常數的一種數列，常用G、P表示。這個常數叫做等比數列的公比，公比通常用字母q表示(q≠0)，等比數列a₁≠ 0。其中{aₙ}中的每一項均不為0。註：q=1 時，aₙ為常數列。等比故事 根據歷史傳說記載，西洋棋起源於古印度，至今見諸於文獻...
- 數列通項公式
等比數列 對於一個數列 {aₙ}，如果任意相鄰兩項之商（即二者的比）為一個常數，那么該數列為等比數列，且稱這一定值商為公比 q ；從第一項a₁ 到第n項aₙ 的總和，記為Tₙ 。那么， 通項公式為 (即a₁ 乘以q 的 （n-1)次方，其推導為“連乘原理”的思想：a₂=a₁ * q,a₃= a...
- 等比數列公式
等比數列公式就是在數學上求一定數量的等比數列的和的公式。另外，一個各項均為正數的等比數列各項取同底指數冪後構成一個等差數列；反之，以任一個正數C為底，用一個等差數列的各項做指數構造冪Can，則是等比數列。背景故事 根據歷史傳說記載，西洋棋起源於古印度，見諸於文獻最早的記錄是在薩珊王朝時期用波斯文...
- 數列
若為等差數列，且有aₙ=m，aₘ=n，則a=0。其於數學的中的套用，可舉例：快速算出從23到132之間6的整倍數有多少個，算法不止一種，這裡介紹用數列算令等差數列首項a₁=24（24為6的4倍），等差d=6；於是令aₙ= 24+6(n-1)等比數列 定義 一般地，如果一個數列從第2項起，每一項與它的前一項...
- 數列求和
數列是高中代數的重要內容，又是學習高等數學的基礎。在高考和各種數學競賽中都占有重要的地位。數列求和是數列的重要內容之一，除了等差數列和等比數列有求和公式外，大部分數列的求和都需要有一定的技巧。公式法 等差數列求和公式:（首項+末項）×項數/2 舉例：1+2+3+4+5+6+7+8+9+10=（1+10）×10/2=55...
- 等差數列
等差數列是指從第二項起，每一項與它的前一項的差等於同一個常數的一種數列，常用A、P表示。這個常數叫作等差數列的公差，公差常用字母d表示。例如：1,3,5,7,9……2。通項公式為：aₙ=a₁+(n-1)×d。首項a₁=1，公差d=2。前n項和公式為：Sₙ=na₁+n×(n-1)×d/2或Sn=n×(a₁+...
- 等差數列公式
等差數列是常見的一種，如果一個數列從第二項起，每一項與它的前一項的差等於同一個常數，這個數列就叫作等差數列，而這個差，公差常用字母d表示。例如：1,3,通項公式推導：a₂-a₁=d;a₃-a₂=d;a₄-a₃=d……aₙ-a=d,將上述式子左右分別相加，得出aₙ-a₁=(n-1)*d→aₙ=a...
- 差比數列求和公式
差比數列是由一個等差數列和一個等比數列相乘得到的新數列，其求和是高中數學常考內容。但學生在利用錯位相減法進行差比數列求和時，往往只能寫出前幾步，整理不出最終結果。內容簡介 差比數列求和公式的內容：題目：求數列的前項和。公式：結構分析：。此公式看似複雜，實際上結構簡單。僅需對結構配上4個係數即可。
- 專題王高中數學:數列
規避易錯點。圖書目錄 第1講 數列的概念與簡單表示法 本講達標訓練 第2講 等差數列 2.1 等差數列 2.2 等差數列的性質 本講達標訓練 第3講 等比數列 3.1 等比數列 3.2 等比數列的性質 本講達標訓練 第4講 數列的求和與套用 4.1 數列的求和 4.2 數列的綜合套用 本講達標訓練 第5講 高頻考點闖關 ...
- 雙重數列
定義：數列中每兩項之間存在等比或者等差等關係的數列叫做雙重數列。雙重數列是指兩個數列交替排在一起而形成的一種數列,位於奇數項的數字構成一種規律,位於偶數項的數字構成另一種規律.例如:1,2,4,4,16,6,64 ...奇數項為：1,4,16,64; 1=1²,4=2²,16=4²,64=8².偶數項為：2,4,6,（...
- 高中數學題典:數列
《高中數學題典：數列》可供高三師生複習備考時使用，也可供參加全國高中數學聯賽和自主招生的同學和教練員使用。同時，書中的試題還可方便老師在教學和編擬試題時選用。目錄 第1章 數列的概念及表示法 第2章 等差數列 第3章 等比數列 第4章 數列求和 第5章 求數列通項公式 第6章 數列綜合問題 ...
- 高中數學300題:數列與數學歸納法
《交大之星·高中數學300題:數列與數學歸納法》是課堂學習和高考應試複習的理想用書，適用於高中學生和高中數學老師。圖書目錄 第一章 等差、等比數列概念和性質 1 一、數列的概念 1 二、等差數列的定義和通項公式 5 三、等差數列求和 8 四、等差數列的性質 12 五、等比數列的定義和通項公式 15 六、等比數列...
- 專題小課本·專題全解:高中數學·數列
第二章 等差數列(35)第一單元 等差數列(35)方法·技巧 整體思想(39)/方程思想(40)/函式思想(40)/化歸思想(41)第二單元 等差數列的前n項和(45)方法·技巧 方程思想(51)/整體思想(52)/分類討論思想(52)本章綜合提升(57)第三章 等比數列(68)第一單元 等比數列(68)方法·技巧 整體思想(73)/方程思想(74...
- 高中數學經典題型全解析:數列與導數
3．3等差、等比數列套用題(53)3．4數學歸納法的基本原理(58)3．5數學歸納法的處理策略(61)3．6常見的放縮法策略(63)第2篇數列通項與求和公式 第4課求數列的通項公式的常見題型(66)4．1作差法由前n項和Sn求數列通項公式(66)4．2疊加法求an－an－1=f(n)型差數列的通項公式(72)4．3疊乘法求an=...
- 數列·遞推·遞歸
《數列·遞推·遞歸》是該叢書中的一種.它從數列的概念和最基本的數列——等差數列和等比數列研究開始，分別 對與等差數列、等比數列有關的差分數列、等比差數列、循環 數列、分群數列等進行研究，特別是對數列求和以及數列不等 式的種種問題進行了詳細地歸納研究。內容介紹 利用遞推公式和遞推關係導出的遞歸數列...
- 數和數列
《數和數列》是2016年科學出版社出版的圖書，作者是孫智宏。內容簡介 本書共分21講，由淺入深，系統介紹了數、數列和初等數論的知識及數論學家的故事，討論了中學生需要掌握的複數、數學歸納法、等差數列、等比數列、 組合數與二項式定理，參加數學競賽需要掌握的取整函式與抽屜原理、數的整除與一次不定方程、算術基本...
- 遞推公式
等比數列遞推公式：bₙ=q(n-1)*b （q為公比 b為首項）由遞推公式寫出數列的方法：1. 根據遞推公式寫出數列的前幾項，依次代入計算即可；2.若知道的是末項，通常將所給公式整理成用後面的項表示前面的項的形式。遞推列 亦稱遞歸列。由前面的項能推出後面的項的數列。指對所有n>p，滿足形如aₙ=f(...
- 數字推理(行政測試中的題型)
選B。和差與立方關係組合。0=1的3次方-1，6=2的3次方-2，24=3的3次方-3，60=4的3次方-4，120=5的3次方-5。1，4，8，14，24，42，（ ）A 76 B 66 C 64 D68 選A。兩個等差與一個等比數列組合 依次相減，得3，4，6，10，18，（ ）再相減，得1，2，4，8，（ ），此為等比數列，下一...
- 通項公式
3)等差數列{aₙ}的公差d可由公式d=(aₙ-aₘ)/(n-m)確定。例3 在100以內有多少個能被7整除的自然數？解 100 以內能被7整除的自然數構造一個等差數列，其中a₁=7，d=7.由 可得 又因為n∈N，所以在100以內共有14個能被7整除的自然數。等比數列通項公式 如果等比數列{aₙ}的首項為a₁，...
- 分組求和法
分組求和法:就是將數列的項分成二項，而這兩項往往是常數或是等差（比）數列，進而利用等差數列或等比數列的求和方法分別求和，然後再合併，從而得到該數列的和。常見類型 (1)若an=bn±cn，且{bn}，{cn}為等差或等比數列，可採用分組求和法求{an}的前n項和．(2)通項公式為an=bn (n為奇數)；cn (n為...
- 新課標數學解析(高二上)(第二版)
第七章 數列與數學歸納法 一 數列 7.1 數列的概念（1）7.1 數列的概念（2）7.2 等差數列（1）7.2 等差數列（2）7.2 等差數列（3）7.3 等比數列（1）7.3 等比數列（2）7.3 等比數列（3）7.3 等比數列（4）數列單元測驗題 二 數學歸納法 7.4 數學歸納法的概念 7.5 數學歸納法的套用 7.6 ...
- 數值分級制度
一般數值系列有等差數列 (常用於日常生活用品及軸承、緊固件的參數分級)、等比數列及其他尚未標準化的數值系列。優先數系具有以下幾個特徵： (1) 簡單易記。(2) 數值分級成等比。這樣可以確定適當的參數間隔。(3) 使用數值的優先順序是固定的，即按R5、R10、R20、R40和R80數列的順序使用數值，有利於產品間的協調...
- 數學(選擇性必修第2冊RJA)/學霸題中題
第四章 數列 4．1 數列的概念 4．1 強化訓練 4．2 等差數列 4．2．1 等差數列的概念 4．2．2 等差數列的前n項和公式 課時1 等差數列的前n項和及其性質 課時2 等差數列的前n項和的綜合套用 4．2 強化訓練 4．3 等比數列 4．3．1 等比數列的概念 4．3．2 等比數列的前n項和公式 課時1 等比數列...
