基本介紹
- 中文名:積分流形
- 外文名:integral manifold
- 領域:數學
- 性質:子流形
- 定義:對合分布確定的子流形
- 空間:切空間
概念,流形,對合分布,微分流形,切空間,
概念
積分流形(integral manifold)是一類子流形。它是由對合分布確定的子流形。設Dl是Ck流形M上的l維分布,包含映射i:W→M為浸入。若對於每一點p∈W都有i*(Tp(W)) Dl(p),即i的切映射將子流形(W,i)在p點的切空間Tp(W)映入Dl(p)中,則稱(W,i)或i(W)是Dl的積分流形。當一個積分流形不能成為其他的積分流形的真子集時,稱它為極大積分流形。在坐標鄰域U上任取屬於D的一個向量場,則它的任一條積分曲線都是D的1維積分流形。特別地,設D為C分布且對每個點p都存在p點的坐標圖(U,φ,x),使得
Dl(p),即i的切映射將子流形(W,i)在p點的切空間Tp(W)映入Dl(p)中,則稱(W,i)或i(W)是Dl的積分流形。當一個積分流形不能成為其他的積分流形的真子集時,稱它為極大積分流形。在坐標鄰域U上任取屬於D的一個向量場,則它的任一條積分曲線都是D的1維積分流形。特別地,設D為C分布且對每個點p都存在p點的坐標圖(U,φ,x),使得

Uc={q∈U|xα(q)=cα,cα為常數,l+1≤α≤n}
都是Dl的積分流形,即Dl在U上由:

所生成時,稱Dl是完全可積的。
流形
流形是一類拓撲空間,它在每一點的附近都與歐氏空間同胚。一般的流形概念,起始於對於可微流形的研究,在點集拓撲中已經熟悉把一元或多元連續函式的概念,推廣為拓撲空間之間連續映射的概念。但是對於函式的可微性,在進行類似的推廣時,卻遇到截然不同的情況,若M,N為拓撲空間,f:M→N為映射,則為了計算微商,須考慮(f(x+h)-f(x))/h,然而在一般空間中,這是沒有意義的,因此對於M與N,提出了有一個支撐空間的要求,這是產生可微流形概念的客觀要求。
在歷史上,n維流形的概念在拉格朗日(Lagrange,J.-L.)時代已初見端倪,黎曼(Riemann,G.F.B.)於1854年利用參數的觀點,對維數用歸納法進行構造,以後龐加萊(Poincaré,(J.-)H.)為了擺脫這種研究方法的複雜性,把n維流形定義為這個樣子,即它是一種連通的拓撲空間,其中每點有一個鄰域與R(或C)的一個鄰域同胚,即把流形定義為局部歐氏空間。這是曲線與曲面概念的高維推廣,它是代數拓撲、微分拓撲、幾何拓撲以及微分幾何研究的主要對象。
對合分布
對合分布是一類特殊的分布。Ck流形M上l維對合分布Dl具有下述的特徵性質:對於M的每一個點,都有一個鄰域U及Dl在U上的一組Ck-1局部基向量場X1,X2,…,Xl,使得[Xi,Xj](1≤i,j≤l)在U上都屬於Dl。這時也稱分布D是對合的.[Xi,Xj]屬於Dl等價於它們都是X1,X2,…,Xl的線性組合,即[Xi,Xj]=μijXh,μij∈C(U) (i,j,h=1,2,…,l).能選到一組局部基向量場使得μhij≡0。分布是對合的也意味著對於任意兩個屬於Dl的Cr向量場X,Y,其李括弧[X,Y]也屬於Dl。
微分流形
具體說來,設M是一個Hausdorff空間。U是M的開集,h是U到n維歐氏空間R的開集(常取為單位球內部或立方體內部等等)上的一個同胚映射,則(U,h)稱為一個坐標圖,U稱為其中點的一個坐標鄰域。設M為開集系{Uα}所覆蓋,則(Uα,hα)的集合稱為M的一個坐標圖冊。如果M的坐標圖冊中任何兩個坐標圖都是C相關的(坐標圖冊應該是極大的,即若任一坐標圖與坐標圖冊中每一個坐標圖都相容則其自身也屬於坐標圖冊),則稱M有C微分結構,又稱M為n維的C微分流形。C相關是指流形M上同一點的不同坐標之間的變換關係是C可微分的(k=0,1,…,∞或ω),依通常記號C表示解析函式。具體來說, 如p∈Uα∩Uβ,(x,)(x)(i=1,…,n)分別是p在兩個坐標圖(Uα,hα),(Uβ,hβ)下的(局部)坐標,即那么它們之間的關係式可表為而ƒ關於x(j=1,2,…,n)具有直到k次的連續導數。k=0時,M是拓撲流形;k>0時,就是微分流形;k=ω時,是解析流形。C流形又常稱為光滑流形。如果微分流形M是一個仿緊或緊緻拓撲空間,則稱M為仿緊或緊緻微分流形。如果可選取坐標圖冊使微分流形M中各個坐標鄰域之間的坐標變換的雅可比行列式都大於零,則稱這個流形是可定向的。球面是可定向的,麥比烏斯帶是不可定向的。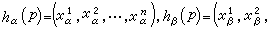 1
1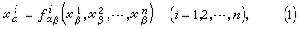 2
2
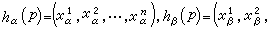 1
1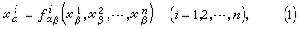 2
2同一拓撲流形可以具有本質上不同的微分結構。米爾諾(John Milnor)首先發現作為一個拓撲流形,七維球面上可有不同於標準微分結構的怪異微分結構。後來弗里德曼(Michael Freedman)等得出如下的重要結果:四維歐氏空間中也有多種微分結構,這與其他維數的歐氏空間只有惟一的微分結構有著重大區別。
切空間
切空間是微分流形在一點處所聯繫的向量空間,歐氏空間中光滑曲線的切線、光滑曲面的切平面的推廣。若M是n維微分流形,p∈M,記C∞(p)為在p的某個鄰域內有定義的C∞可微函式的集合,則適合下列條件的函式Xp:C∞(p)→R稱為M在p處的切向量:
1.對於f,g∈C∞(p),若存在M中p的某鄰域U,使得f|U=g|U,則Xp(f)=Xp(g).
2.對於f,g∈C∞(p),α,β∈R,有:

(αf+βg)(q)=αf(q)+βg(q)∈R,當f(q),g(q)有定義時。
3.對於f,g∈C(p),有:Xp(f×g)=f(p)Xp(g)+g(p)Xp(f),
其中f×g是通常函式的乘法,即:(f×g)(q)=f(q)g(q)。
微分流形M在p∈M處的全體切向量的集合記為TpM,對於Xp,Yp∈TpM,α∈R與f∈C∞(p),設:


因而TpM是實數域R上的n維向量空間,稱為微分流形M在p處的切空間。
切空間TpM中切向量的表示:設(U,φ)是M含點p的卡,在U上局部坐標為:
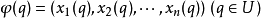


其中(u1,u2,…,un)是R^n中坐標,則:

並且:

是TpM的一組基。此時對於Xp∈TpM,有:

