基本介紹
- 中文名:相切
- 外文名:tangency
- 所屬領域:數理科學
- 學科:幾何學
- 分類:圓與直線、圓與圓,圓與多邊形等
圓與圓相切
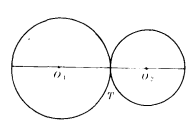 圓與圓相切(a)
圓與圓相切(a)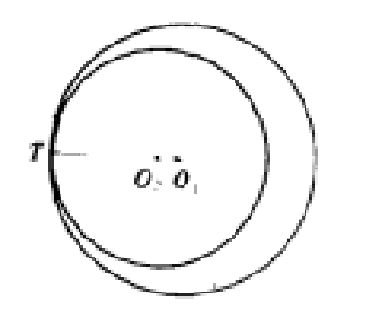 圓與圓相切(b)
圓與圓相切(b)圓與直線相切
 圓與直線相切
圓與直線相切圓與多邊形相切
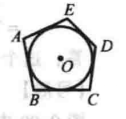 圓與多邊形相切
圓與多邊形相切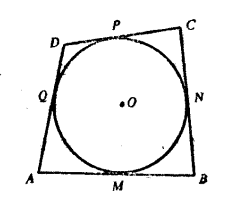 圓與多邊形相切
圓與多邊形相切
 圓與圓相切(a)
圓與圓相切(a) 圓與圓相切(b)
圓與圓相切(b) 圓與直線相切
圓與直線相切 圓與多邊形相切
圓與多邊形相切 圓與多邊形相切
圓與多邊形相切相切是平面上的圓與另一個幾何形狀的一種位置關係。若直線與曲線交於兩點,且這兩點無限相近,趨於重合時,該直線就是該曲線在該點的切線。國中數學中,若一條直線...
兩圓相切(contact of two circles)兩圓間的一種位置關係.指兩圓只有惟一的公共點.惟一的公共點稱為切點。與一般的平面二次曲線相比,由於圓所具有的旋轉對稱性,...
數學領域的詞語。直線和圓相切,直線和圓有唯一公共點,叫做直線和圓相切。可以通過比較圓心到直線的距離d與圓半徑r的大小、或者方程組、或者利用切線的定義來證明。
兩圓與同圓相切(simultaneous contact of acircle with two circles)兩圓的公切圓.指兩圓同時與第三個圓相切.這種相切可分同態相切和異態相切兩種.同態相切是指...
球與平面相切(contact between a sphere and aplane)球與平面的一種特殊位置關係.球與平面有且僅有一個公共點時,球與平面的位置關係...
兩球相切(contact between two spheres)兩球間的一種特殊位置關係.指兩球有惟一的公共點的位置關係.這時,如果一球在另一球的內部,則稱為兩球內切.如果一球在...
球與直線相切(contact between a sphere and aline)球與直線的一種特殊位置關係.當球與直線只有一個公共點時,球與直線的位置關係稱為相切.這直線稱為球的切線,...
三重相切圓是與三角形相關的一組圓。三角形的內切圓與三個旁切圓都分別和三角形的三條邊(或邊的延長線)相切,它們統稱為三角形的三重相切圓。...
對於標準狀態下的圓錐曲線和直線的相切狀態由一個比較簡單的判定公式:設直線的方程為Ax+By+C=0:當圓錐曲線為橢圓b^2x^2+a^2y^2=a^2b^2時...
如果一個多邊形(或多面體)的每一邊(或多面體之每一面)均與位於其內的一條閉曲線(或曲面)相切,則稱此多邊形(或多面體)外切於該曲線(或曲面)。...
公切線是指同時相切於兩條或兩條以上的曲線的直線,例如和兩個圓相切的直線叫做這兩個圓的公切線。如果兩個圓在公切線的同側,則這公切線叫外公切線;如果兩個...
弦切角定理:弦切角的度數等於它所夾的弧所對的圓心角度數的一半,等於它所夾的弧所對的圓周角度數。與圓相切的直線,同圓內與圓相交的弦相交所形成的夾角叫做弦切角...
若兩個幾何圖形在某個地方有且只有有一個交點,則可以稱為相切而不是相交。如果兩個圖形完全重合,則一般不稱為相交。 [1] 集合論中,兩個集合相交是指它們的...
與截面相切的應力稱為剪應力或切應力,與正應力相對。...... 應力的量值等於單位面積上內力量值。同截面相切的力稱為剪應力或切應力。切應力簡介 編輯 在液體層流...
頂點在圓上,一邊和圓相交,另一邊和圓相切的角叫做弦切角。其大小等於它所夾的弧所對的圓周角。...
a1j1與無差異曲線相切於E1點。與E1點相對應的x商品的購買量是q1。收入效應:一種商品價格變化的收入效應是指在其他所有商品的名義價格與名義收入不變的情況下,...
其中設定1線為夏至日時間點的晨昏線(圈),它將地球上的緯度線相切成交角為正負23.26度,構成了夏至日的北極圈成極晝;南極圈成極夜。設定3線為冬至日時間點的...
關於內切圓和外切圓:只有兩圓相切時,才有內切圓和外切圓之說。兩圓心之間距離為兩圓半徑之差的是內切圓,兩圓圓心距離為兩圓半徑之和的為外切圓。即,當且...
與多邊形各邊都相切的圓叫做多邊形的內切圓。特殊地,與三角形三邊都相切的圓叫做三角形的內切圓,圓心叫做三角形的內心,三角形叫做圓的外切三角形。三角形的內心...
