如果兩個圓只有一個公共點,且圓心的距離等於兩個圓半徑的和,則這兩個圓互為外切圓。
基本介紹
- 中文名:外切圓
- 外文名:externally tangent circle
- 公切線:兩圓外切時,有3條公切線
- 針對:另一個圓來說的
- 套用學科:幾何學
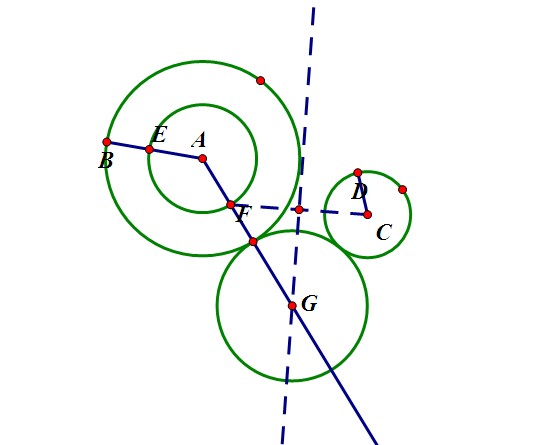
如果兩個圓只有一個公共點,且圓心的距離等於兩個圓半徑的和,則這兩個圓互為外切圓。
如果兩個圓只有一個公共點,且圓心的距離等於兩個圓半徑的和,則這兩個圓互為外切圓。...
圓的外切多邊形:如果一個圓是一個多邊形的內切圓,多邊形所有的邊都和一個圓相切,這個多邊形叫做這個圓的外切多邊形,這個圓叫做多邊形的內切圓。...
每個三角形都有三個外切圓,外切圓半徑公式分別為:Ra = 2S/(b+c-a)Rb = 2S/(a+c-b)Rc = 2S/(a+b-c)備註:S為該三角形的面積;Ra為與a邊相切的...
圓外切正多邊形(circumscribed regular poly-gon of circle)一類重要的正多邊形。指各邊都切於同一圓的正多邊形。正多邊形總外切於圓,故稱為圓外切正多邊形,該...
各邊都和圓相切的三角形叫做圓的外切三角形。做任意三條切線,然後延長至三條線相交,此三角形則為所求。...
圓外切多邊形(circumscribed polygon of a circle)與圓相關的一種多邊形.指各邊與同一圓相切的多邊形.此圓稱為多邊形的內切圓. ...
外切密率(Waiqie milu )《求表捷術》中的一種.四卷,清戴煦撰,成書於1852年.該書論述了以前中國數學家未曾討論過的正切、餘切、正割、餘割等四種三角函式的...
兩圓與同圓相切(simultaneous contact of acircle with two circles)兩圓的公切圓.指兩圓同時與第三個圓相切.這種相切可分同態相切和異態相切兩種.同態相切是指...
三重相切圓是與三角形相關的一組圓。三角形的內切圓與三個旁切圓都分別和三角形的三條邊(或邊的延長線)相切,它們統稱為三角形的三重相切圓。...
牛頓定理2圓外切四邊形的兩條對角線的中點,及該圓的圓心,三點共線。 定理2證明 證明: 設四邊形ABCD是⊙I的外切四邊形,E和F分別是它的對角線AC和BD的中點...
布里昂雄定理(Brianchon theorem)是射影幾何的著名定理之一,外切於一個非退化二級曲線的簡單六線形的三對對頂點的連線共點,此點稱為布里昂雄點。此定理是布...
相切兩圓分兩圓外切和兩圓內切兩種情況.兩圓外切是指除它們的公共點外,每個圓上的點都在另一個圓的外部(如圖1).兩圓外切的充分必要條件是圓心距等於兩圓...
圓的外切多邊形:如果一個圓是一個多邊形的內切圓,多邊形所有的邊都和一個圓相切,這個多邊形叫做這個圓的外切多邊形,這個圓叫做多邊形的內切圓 [4] 。...
