圓與圓外切
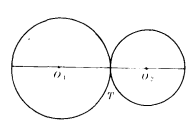 圖1(a) 圓與圓外切
圖1(a) 圓與圓外切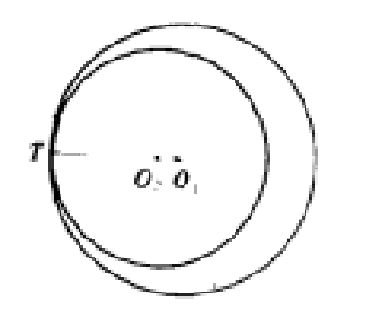 圖1(b) 圓與圓內切
圖1(b) 圓與圓內切兩個圓只有一個公共點就叫做兩圓相切,公共點叫做
切點,兩圓相切有兩種:
(1)兩圓外切,如圖1(a);
連線兩圓中心的直線叫做
連心線,當兩圓相切時,切點在連心線上。
兩圓外切時,圓心距O1O2=R﹢r,(設大圓的半徑為R,小圓的半徑為r)。
兩圓內切時,圓心距O1O2=R﹣r。
相切兩圓的連心線或其延長線,必經過切點。
如圖(a)中,⊙O1,和⊙O2相切於點T,則連心線O1O2必過點T。
如圖(b)中,⊙O1,和⊙O2相切於點T,則連心線O1O2的延長線必過點T。
圓與多邊形外切
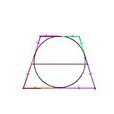
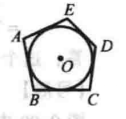 圖2 圓與多邊形相切
圖2 圓與多邊形相切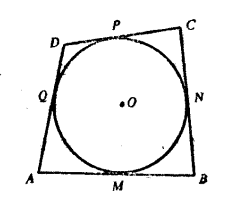 圖3 圓與多邊形相切
圖3 圓與多邊形相切圓的外切
多邊形:如果一個圓是一個多邊形的
內切圓,多邊形所有的邊都和一個圓相切,這個多邊形叫做這個圓的外切多邊形,這個圓叫做多邊形的內切圓。
如圖,五邊形ABCDE就是圓O的外切五邊形。
例如,圖中的四邊形ABCD是⊙O的外切四邊形,而⊙O是四邊形ABCD的內切圓。
兩球外切
設有兩球, 其球心分別為
,半徑分別為
,中心距離
;於是有:
1.
時,兩球只有—,個公共點,此公共點在連心緩上。如果過這個公共點,作與連心線相垂直的平面,則兩球分刈在此平面的兩側,它們都和這平面相切,這樣的兩個球,稱為
兩球外切。
2.
時, 兩球只有一個公共點, 此公共點在連心線的延長線上,如果經過這個公共點,作一平面和連心綾相垂直,則兩球在A1:平面的同側,它們都和這平面相叨,這樣的兩個球稱為
兩球內切。
3.
時, 兩球沒有公共點, 其中一球上的所有的點都在另一球的裡面,另一球上的所有的點郎在這一球的外面,這樣的兩個球稱為
兩球內離。
4.
時,兩球沒有公共點。其中任何一球上的所有的點,均在另一球的外面,這樣的兩個球稱為
兩球外離。
5.
時; 兩球有無數公共點, 這些公共點構成一個圓,這樣的兩個球稱為
相交。
球的外切多面體
多面體的內切球是滿足特定條件的一個球,如果一個球與簡單多面體的各面或其延展部分都相切,且此球在多面體的內部,則稱這個球為此多面體的內切球,多面體稱為這個球的外切多面體。正多面體的內切球均存在,正多面體內任意點到各面距離之和為常數3FV/S,這裡F為多面體的面數,S為表面積,V為體積,故正多面體內切球半徑為3V/S。
其他外切情況舉例
柱的外切稜柱
柱的外切稜柱(circumscribed prism of a cylinder)是一個與已知柱有關的稜柱。滿足下述條件的稜柱,稱為柱的外切稜柱(柱稱為稜柱的內切柱):
1.稜柱的兩底分別是柱的相應底面的外切多邊形(即稜柱底面的邊與柱底面邊界線相切);
2.稜柱的側棱與柱的母線平行且相等。
錐的外切稜錐
錐的外切稜錐(circumscribed pyramid of a cone)是一個與已知錐面有關的稜錐,即與錐相外切的稜錐。滿足下述條件的稜錐,稱為錐(體)的外切稜錐(錐則稱為稜錐的內切錐):
1.稜錐的底面多邊形外切於錐的底面曲線;
2.稜錐與錐共頂點。
 圖1(a) 圓與圓外切
圖1(a) 圓與圓外切 圖1(b) 圓與圓內切
圖1(b) 圓與圓內切 圖2 圓與多邊形相切
圖2 圓與多邊形相切 圖3 圓與多邊形相切
圖3 圓與多邊形相切