基本介紹
- 中文名:球面圖形
- 外文名:spherical figure
- 所屬學科:數學
- 所屬問題:球面幾何
- 概念:所有點都在同一球面上的幾何圖形
- 舉例:球面大圓、小圓、球面多邊形等
基本介紹
球面圖形的基本元素
其他球面圖形及性質













































































球面圖形(spherical figure)是球面幾何的研究對象,指所有點都在同一球面上的幾何圖形,在球面幾何學中,主要研究的球面圖形有球面大圓、小圓、球面多邊形、球面二角形和球面三角形等。基本介紹與空間一點O有等距離R...
球面多邊形(spherical polygon)是一種特殊的球面圖形,在球面上依次給出有限個點A₁,A₂,…,Aₑ(e>2),其中相鄰三點都不共大圓,依次用劣大圓弧A₁A₂,A₂A₃,…,AnA₁將它們連結,所圍成的球面圖形(在相鄰...
球面角 球面角(spherical angle)是一種特殊的球面圖形,指由球面上一點和以此點為公共端點的兩條大圓弧所構成的球面圖形,公共端點稱為該球面角的頂點,兩條大圓弧稱為該球面角的邊。若球面角的頂點是A,它的兩條邊分別通過點B,C(...
儘管在數學之外,術語“球面”和“球”有時可互換使用,但在數學中是明確區分的:球面是一種嵌在三維歐幾里得空間內的二維封閉曲面,而球是一種三維圖形,其包括球面和球面內部的一切(閉球),不過更常見的定義是只包括球面內部的所有...
全等球面圖形(congruent spherical figures)兩球面圖形的一種等價關係 全等球面圖形(congruent spherical figures)兩球面圖形的一種等價關係.若圖形F和F'在同一球面或等球面上,且它們的點之間可建立一一對應關係,使得以F的任意兩點為端點的...
球面多邊形 (spherical polygon)球面多邊形是一種特殊的球面圖形,在球面上依次給出有限個點A₁,A₂,…,Aₑ(e>2),其中相鄰三點都不共大圓,依次用劣大圓弧A₁A₂,A₂A₃,…,AnA₁將它們連結,所圍成的球面...
從大圓弧或小圓弧上的一點到極的球面角距稱為極距。顯然,同圓上任一點的極距都相等。大圓的極距等於90°。極距等於90°的大圓弧稱為極線或稱為赤道。球面角:球面上一點及過該點的任意兩條大圓弧所構成的圖形稱為球面角,該點稱為...
當a=b=c時,即三個半軸都相等時,為球面:。相關概念 橢球面關於三坐標平面、三坐標軸、坐標原點都對稱. 橢球面的對稱平面、對稱軸與對稱中心依次叫做橢球面的主平面、主軸與中心.橢球面的三條對稱軸與橢球面的交點叫做橢球面的...
如圖2,設在同球面或等球面上,如果在兩個球面三角形ABC和A'B'C'中,AB=A'B',AC=A'C',∠A=∠A’,要判斷這兩個球面三角形是否全等,可以用重合法。我們在平面幾何里也常用重合法進行證明,就是通過移動把一個圖形轉移到與...
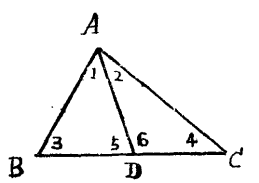
從上面的討論可以概括出下述結果:如果以球面角的頂點為極作大圓,則球面角的邊或其延長線在這個大圓上所截取的那個弧段便是球面角的數值。球面三角形:把球面上的三個點用三個大圓弧聯結起來,所圍成的圖形叫做球面三角形。這三個大...
4) 如果在平面ABC上,極限球面的軸BB’介於兩軸AA'和CC’之間,我們說:在直道線ABC上,點B介於點A和點C之間。5)所謂圖形的“運動”是僅指那些運動,當運動時,圖形的各點經常保留在已知的極限球面上。我們現在來列舉一些命題,在...
球面區域簡稱球面域,是一類特殊的球麵點集。簡介 球面區域簡稱球面域,是一類特殊的球麵點集。若一球面圖形 F 將球面上所有不屬於 F 的點分為具有下列性質的 A,B 兩類,則 A,B 兩類點各自所組成的點集分別稱為球面區域:1.同類...
黎曼球面由19世紀數學家黎曼而得名。從代數角度來說,複數加上一個無窮遠點構成一個數系,稱為擴充複數。無窮遠點的算數有時和一般的代數規則不符,因此擴充複數不構成一個代數域。但是,黎曼球面在幾何和解析角度都行為良好,甚至在...
由不在同一直線上的三條線段首尾順次連線所組成的封閉圖形叫做三角形。 平面上三條直線或球面上三條弧線所圍成的圖形。 三條直線所圍成的圖形叫平面三角形;三條弧線所圍成的圖形叫球面三角形,也叫三邊形。內角 內角和為180° 直...
《航海帶來的啟發:球面上的幾何》是2014年貴州人民出版社出版的圖書。內容簡介 球面幾何是研究球面上圖形幾何性質的一門學科,自古希臘開始發展,到15世紀才獨立於天文學成為一門獨立學科,在當今社會的科學技術套用中有著重要意義。項昭...
球體是一個連續曲面的立體圖形,由球面圍成的幾何體稱為球體。世界上沒有絕對的球體。絕對的球體只存在於理論中。但在失重環境(如太空)中,液滴自動形成絕對球體。球體的組成 球的表面是一個曲面,這個曲面就叫做球面。球和圓類似,...
月形(Tune)有兩種指代,它可以指一種特殊的平面圖形,即同一平面上兩條圓弧之間的(平面)部分,也可以指一種球面圖形,即“球面二角形”。平面中的月形 基本概念 平面中的月形是一種特殊的平面圖形,指有相同的底,且在底的同一側...
大圓被定義為過球心的平面和球面的交線。大圓的圓心與球心重合,半徑與球的半徑相等。大圓是球面上最大的圓,與小圓相對。簡介 大圓是球面幾何的基礎知識,被定義為過球心的平面和球面的交線。如果平面不過球心,則它和球面的交線定...
一個球形拼圖,也稱為“立體拼圖,球體拼圖”。與傳統拼圖不同的是,它是球形立體的,而不是我們常見到的平面圖形。一種球形拼圖,包括一由二半球組成的球體及多塊拼片,拼片的數量至少可拼組成一完整的球面,各拼片具有可相互拼合的...
它是球面的一部分,是球面被一個平面截成的,球冠的任何部分都不能展開成平面圖形。公式 球面被平面所截得的一部分叫做球冠。截得的圓叫做球冠的底,垂直於截面的直徑被截得的一段叫做球冠的高。球冠也可以看成一段圓弧繞經過它的一...
平面圖形 任何平面圖形都可以視為一個二面體,並且屬於二面體群。若將一封閉的平面圖形放置於三維空間也可以視為一個二面體,如多邊形二面體。他們皆屬於二面體群,是透鏡空間的基本域。球面鑲嵌 二面體可以以球面鑲嵌的方式存在,最...
幾何圖形的分類問題(比如把圓錐曲線分為三類),也就轉化為方程的代數特徵分類的問題,即尋找代數不變數的問題。立體幾何歸結為三維空間解析幾何的研究範疇,從而研究二次曲面(如球面,橢球面、錐面、雙曲面,鞍面)的幾何分類問題,就...
儘管在數學之外,術語“球面”和“球”有時可互換使用,但在數學中是明確區分的:球面是一種嵌在三維歐幾里得空間內的二維封閉曲面,而球是一種三維圖形,其包括球面和球面內部的一切(閉球),不過更常見的定義是只包括球面內部的所有...
