斜角球面三角形

斜角球面三角形(oblique angled spherical triangle)是球面三角形的一種，指三個內角都不是直角的球面三角形。三個內角都是銳角的斜角球面三角形，稱為銳角球面三角形；至少有一個內角是鈍角的斜角球面三角形，稱為鈍角球面三角形。

基本介紹

• 中文名：斜角球面三角形
• 外文名：oblique angled spherical triangle
• 所屬學科：數學（球面幾何）
• 屬性：一種球面三角形
• 定義：三個內角都不是直角的球面三角形
• 分類：銳角、鈍角球面三角形

基本介紹

定義

斜角球面三角形指三個內角都不是直角的球面三角形。三個內角都是銳角的斜角球面三角形，稱為銳角球面三角形；至少有一個內角是鈍角的斜角球面三角形，稱為鈍角球面三角形。

球面三角形

將球面上的三個點用大圓弧連線起來所圍成的圖形稱為球面三角形，這三個點稱為球面三角形的頂點，三個大圓弧稱為球面三角形的邊，球面三角形的角就是三個大圓弧兩兩相交而成的球面角。

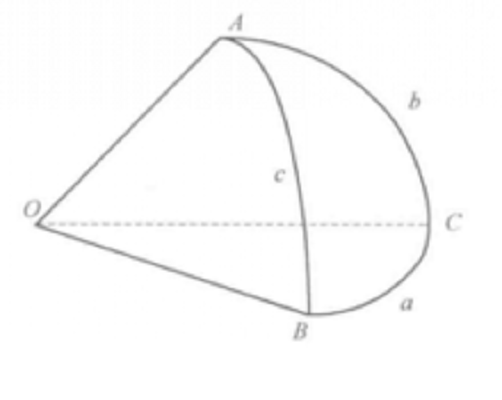
由於連線兩點的大圓弧有兩個不同弧段，將球面上三個點用三段大圓弧連線起來圍成的圖形方式一般有8種，如表1所示陰影部分和無陰影部分。因此，在一般情況下，由三個點規定的球面三角形共有8個，其中一個球面三角形的三個邊都小於半個圓周，將這樣的球面三角形稱為簡單球面三角形，如表1(a)中的陰影部分所示，簡單球面三角形是經常用到的球面三角形。

表1球面三角形

(a)	(b)
(c)	(d)

如圖1所示，組成簡單球面三角形的三個大圓弧所在平面構成一個三面角，其頂點為球心，而其棱是由球心到球面三角形三個頂點的半徑。三面角的每一個平面角都可以用其相對的球面三角形的邊來度量，而兩個平面之間的夾角，即二面角等於其相應的球面三角形的球面角。

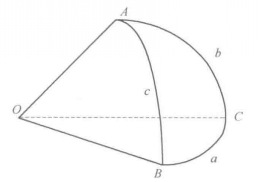
圖1 球面三角形

球面角

球面角(spherical angle)是一種特殊的球面圖形，指由球面上一點和以此點為公共端點的兩條大圓弧所構成的球面圖形，公共端點稱為該球面角的頂點，兩條大圓弧稱為該球面角的邊。若球面角的頂點是A，它的兩條邊分別通過點B，C(如圖2)，則該球面角可以記為∠BAC或∠CAB，球面角的度量有以下三種方法：

1.用由平面AOC和AOB所構成的二面角來度量。

2.用以球面角頂點為極的大圓，被該球面角截得的大圓弧BC之長來度量。

3.用過頂點的兩條邊的切線所夾的角(平面角)∠DAE來度量。

球面角也可以定義銳角、直角或鈍角，小於π/2的球面角稱為銳球面角，等於π/2的球面角稱為直球面角，大於π/2的球面角稱為鈍球面角。

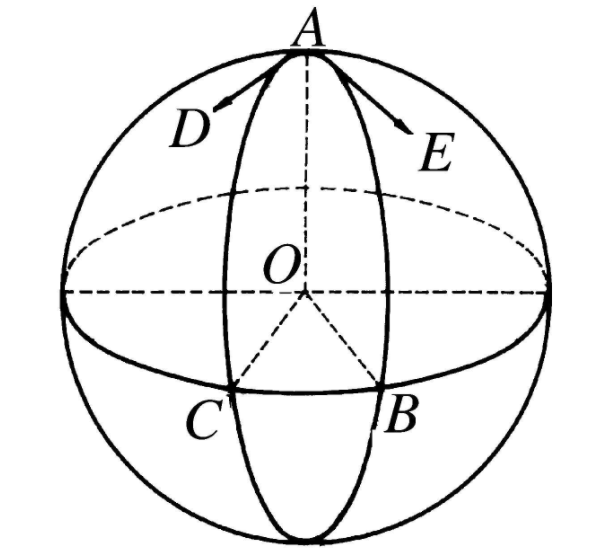
圖2

解法詳解

相關定理及公式

以下規定代表自由球面三角形的邊，為相應的對角，，三角形的面積，E為三角形的球面角盈，是三角形所在的球的半徑，分別為配極三角形相應的元素。

正弦定理：

邊的餘弦定理：

角的餘弦定理：

正切定理：

半角公式：

式中

半邊公式：

式中

高斯公式：

訥皮爾類比：

半正矢公式

確定所求元素的象限的規則

確定斜角球面三角形所求元素的象限的規則：

(a)若，則。

(b)其值距90°最遠的一個邊(角)與其對角(邊)同在一個象限。

(c)任意兩個邊之和的一半與其對角之和的一半在相同的象限。

斜角球面三角形解法小結

表2 斜角球面三角形解法

已知	解法	驗算
三邊	半角公式	正弦定理
三角	半邊公式	正弦定理
兩邊和夾角	先用內皮爾類比(求未知角的和與差)，然後用正弦定理(求其餘的邊)。	高斯公式
兩角和夾邊	先用內皮爾類比(求未知邊的和與差)，然後用正弦定理(求其餘的角)。	高斯公式
兩邊和一對角	正弦定理(求一個角)，然後內皮爾類比(求其餘的角和邊)，注意解的數值。	高斯公式
兩角和一對邊	正弦定理(求一個邊)，然後內皮爾類比(求其餘的邊和角),注意解的數值。	高斯公式