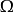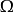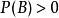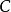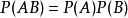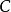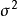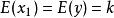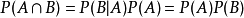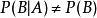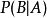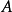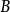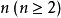獨立同分布變數

在機率統計理論中，隨機過程中，任何時刻的取值都為隨機變數，如果這些隨機變數服從同一分布，並且互相獨立，那么這些隨機變數是獨立同分布，這些變數稱為獨立同分布變數。

獨立同分布最早套用於統計學，隨著科學的發展，獨立同分布已經套用數據挖掘，信號處理等不同的領域。

基本介紹

• 中文名：獨立同分布變數
• 外文名：Independent and identically distributed variables
• 歸屬學科：機率論
• 性質：相互獨立且服從同一分布
• 相關定理：中心極限定理
• 套用：統計學；數據挖掘；信號處理

定義

在機率統計理論中，隨機過程中，任何時刻的取值都為隨機變數，如果這些隨機變數服從同一分布，並且互相獨立，那么這些隨機變數是獨立同分布的，這些變數稱為獨立同分布變數。

性質：

（1）服從同一分布

（2）相互獨立

隨機變數

以一維隨機變數為例：

觀察一個隨機現象，其樣本點可以是具有數量性質的，也可能是非數量性質的，前者如拋一枚骰子，可能出現的點數是1點、2點、...、6點；後者如擲一枚硬幣，可能出現正面，也可能出現反面，現在約定：“出現正面”記為1，“出現反面”記為0。無論是哪一種情形，都體現出這樣的共同點：對隨機試驗的每一個可能結果，有唯一一個實數與之對應。這種對應關係實際上定義了樣本空間 上的函式， ， 。

設 是定義在樣本空間 上的實值單值函式，稱 為一維隨機變數。隨機變數，通常用大寫字母 X,Y,Z,W,...表示

相互獨立

在機率論中，相互獨立，是設 、 是兩事件，如果滿足等式 ，則稱事件 、 相互獨立，簡稱 、 獨立。

設 、 是試驗 的兩個事件，若 ，可以定義 。一般， 的發生對 發生的機率是有影響的，所以條件機率，而只有當 的發生對 的發生沒有有影響的時候才有條件機率 。這時，由乘法定理。

註：若 ， ，則 、 相互獨立與 、 互不相容不能同時成立，即獨立必相容、互斥必聯繫。

推廣：

設 、 、 是三個事件，如果滿足 ， ， ， ，則稱事件、、相互獨立。

更一般的定義是， 是個事件，如果對於其中任意2個、任意3個、…、任意n個事件的積事件的機率，都等於各個事件機率之積，則稱事件 相互獨立。

機率分布

（1）均勻分布

設連續型隨機變數 X 具有機率密度

則稱 X 在區間(a,b)上服從均勻分布，記為

（2）指數分布

設連續型隨機變數 X 具有機率密度

其中， 為常數，則稱 X 服從參數為 的指數分布

（3）常態分配

設連續型隨機變數 X 的機率密度為：

其中， 為常數，則稱X 服從參數為 的常態分配。

例題

已知隨機變數 相互獨立且同分布，方差為 ， ，求 。

解答：

設 ，則有

將下面的式子帶入，很容易得到：