狄利克雷條件是一個信號存在傅立葉變換的充分不必要條件。
狄利克雷條件括三方面:
(1 )在一周期內,連續或只有有限個第一類間斷點;
(2)在一周期內,極大值和極小值的數目應是有限個;
(3)在一周期內,信號是絕對可積的。
基本介紹
- 中文名:狄利克雷條件
- 外文名:Dirichlet Conditions
- 學科:數理科學
- 類型:數學術語
- 作用:傅立葉變換的充分不必要條件
- 提出者:狄利克雷
背景,定義,間斷點,傅立葉變換,
背景
傅立葉在提出傅立葉級數時堅持認為,任何一個周期信號都可以展開成傅立葉級數,雖然這個結論在當時引起許多爭議,但持異議者卻不能給出有力的不同論據。直到20年後(1829年)狄利克雷才對這個問題作出了令人信服的回答,狄利克雷認為,只有在滿足一定條件時,周期信號才能展開成傅立葉級數。這個條件被稱為狄利克雷條件。
定義
狄利克雷條件(Dirichlet Conditions)
(1 )在一周期內,連續或只有有限個第一類間斷點;
(2)在一周期內,極大值和極小值的數目應是有限個;
(3)在一周期內,信號是絕對可積的
一般我們遇到的周期信號都能滿足狄利克雷條件。
狄利克雷條件是一個信號存在傅立葉變換的充分不必要條件。
間斷點
間斷點是指:在非連續函式y=f(x)中某點處xo處有中斷現象,那么,xo就稱為函式的不連續點。間斷點可以分為無窮間斷點和非無窮間斷點,在非無窮間斷點中,還分可去間斷點和跳躍間斷點。如果極限存在就是可去間斷點,不存在就是跳躍間斷點。
幾種間斷點常見類型。
無窮間斷點:函式在該點可以無定義,且左極限、右極限至少有一個不存在,且函式在該點極限為∞。如函式y=tanx在點x=π/2處。
振盪間斷點:函式在該點可以無定義,當自變數趨於該點時,函式值在兩個常數間變動無限多次。如函式y=sin(1/x)在x=0處。
傅立葉變換
傅立葉變換,表示能將滿足一定條件的某個函式表示成三角函式(正弦和/或餘弦函式)或者它們的積分的線性組合。在不同的研究領域,傅立葉變換具有多種不同的變體形式,如連續傅立葉變換和離散傅立葉變換。最初傅立葉分析是作為熱過程的解析分析的工具被提出的。
f(t)是t的周期函式,如果t滿足狄里赫萊條件:在一個以2T為周期內f(X)連續或只有有限個第一類間斷點,附f(x)單調或可劃分成有限個單調區間,則F(x)以2T為周期的傅立葉級數收斂,和函式S(x)也是以2T為周期的周期函式,且在這些間斷點上,函式是有限值;在一個周期內具有有限個極值點;絕對可積。則有下圖①式成立。稱為積分運算f(t)的傅立葉變換,②式的積分運算叫做F(ω)的傅立葉逆變換。F(ω)叫做f(t)的像函式,f(t)叫做F(ω)的像原函式。F(ω)是f(t)的像。f(t)是F(ω)原像。
①傅立葉變換
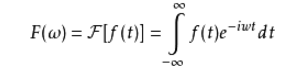
②傅立葉逆變換


