基本介紹
- 中文名:牛頓-萊布尼茨公式
- 外文名:Newton-Leibniz formula
- 分類:數學
- 又名:微積分基本定理
- 時間:1677年
- 提出 :牛頓 萊布尼茨
定理定義
定義




弱化條件






公式推導
推導一













推導二














定理推廣
二重積分形式





曲線積分形式


 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫




發展簡史

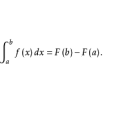
牛頓-萊布尼茲公式一般指本詞條












































 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫





公式套用 牛頓-萊布尼茨公式簡化了定積分的計算,利用該公式可以計算曲線的弧長,平面曲線圍成的面積以及空間曲面圍成的立體體積,這在實際問題中有廣泛的套用,例如計算壩體的填築方量。牛頓-萊布尼茨公式在物理學上也有廣泛的套用,計算運動...
上式便稱為萊布尼茨公式(Leibniz公式)區別 編輯 由於名稱相似,不少人將牛頓-萊布尼茨公式與萊布尼茨公式相混淆,事實上他們是兩個完全不同的公式。 牛頓-萊布尼茨公式是微積分學中的一個重要公式,它把不定積分與定積分相聯繫了起來,也讓...
萊布尼茲公式,也稱為乘積法則,是數學中關於兩個函式的積的導數的一個計算法則。不同於牛頓-萊布尼茨公式,萊布尼茨公式用於對兩個函式的乘積求取其高階導數。萊布尼茨公式是導數計算中會使用到的一個公式,它是為了求取兩函式乘積的高階...
符雲錦. 定積分計算的新公式及其套用. 《 湖南工業大學學報 》 , 2014 駱汝九. 牛頓-萊布尼茨公式的推廣形式. 《 CNKI;WanFang 》 , 2006 張豫岡,王新愛. 牛頓-萊布尼茨公式的一種證明方法. 《 吉林省教育學院學報(上旬) 》...
《用牛頓—布萊尼此公式妙解曲邊圖形的面積》是達拉特旗七中提供的微課課程,主講教師為張曉峰。課程簡介 本作品首先從數學發展歷史和數學文化的角度介紹了兩位偉大的數學家牛頓和萊布尼茨,然後介紹“牛頓-萊布尼茨”公式的具體內容,然後介紹...
拉東-尼科迪姆定理是測度論的重要定理,是牛頓-萊布尼茲公式的推廣。拉東-尼科迪姆導數具有通常點函式導數的某些性質。簡介 拉東-尼科迪姆定理是測度論的重要定理,是牛頓-萊布尼茲公式的推廣。設(Ω,𝓕,μ)是σ有限測度空間,γ是𝓕上...
求某函式的定積分時,在多數情況下,被積函式的原函式很難用初等函式表達出來, 因此能夠藉助微積分學的牛頓-萊布尼茲公式計算定積分的機會是不多的。另外,許多實際問題中的被積函式往往是列表函式或其他形式的非連續函式,對這類函式的...
2 可積函式類3 定積分看作積分上限的函式,牛頓-萊布尼茲公式的再討論4 積分中值定理的再討論5 定積分的近似計算6 瓦利斯公式與司特林公式第十章 廣義積分1 廣義積分的概念2 牛頓-萊布尼茲公式的推廣,分部積分公式與換元積分公式...
定理的第二部分,稱為微積分第二基本定理或“牛頓-萊布尼茨公式”,表明定積分可以用無窮多個原函式的任意一個來計算。這一部分有很多實際套用,這是因為它大大簡化了定積分的計算。該定理的一個特殊形式,首先由詹姆斯·格里高利(1638-...
4.1 定積分概念與牛頓-萊布尼茲公式 4.2 可積條件 4.3 定積分的性質 4.4 變限積分 4.5 反常積分 習題 第五章 級數 5.1 數項級數綜述 5.2 一致收斂概念的提出 5.3 一致收斂判別 5.4 一致收斂函式列(或級數)的性質 習題 習題解...
3.6 定積分的概念、性質和公式 3.6.1 定義和幾何意義 3.6.2 基本性質 3.6.3 牛頓-萊布尼茲公式 3.6.4 直接積分法 3.7 定積分的積分法 3.7.1 “湊微分”法(第一類換元法) 3.7.2 第二類換元法 ...
利用這個規律,在我們了解牛頓-萊布尼茲公式之前,我們便可以對某些函式進行積分。例如:證明對於函式 有 。證明:選擇等比級數來分點,令公比 且 ,那么“矩形面積和”為 提取 ,則有 利用等比級數公式,得到 其中 。設 , 令 ,則...
