基本介紹
- 中文名:牛頓-柯特斯公式
- 外文名:Newton–Cotes formulas
- 分類:數理科學
梯形法則


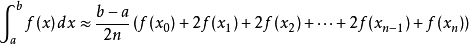
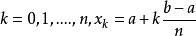
辛普森法則
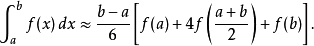

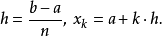
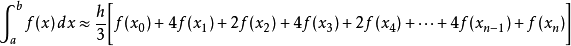
牛頓-柯特斯公式
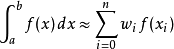

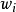

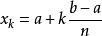


原理
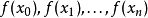

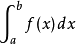




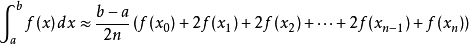
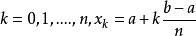
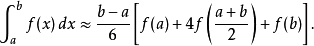

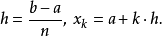
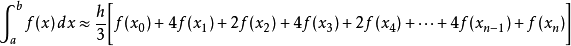
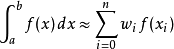

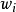

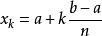


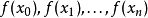

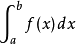


在數值分析上,梯形法則和辛普森法則均是數值積分的方法。它們都是計算定積分的。這兩種方法都屬於牛頓-柯特斯公式。它們以函式於等距n+1點的值,取得一個n次的...
羅傑·柯特斯(Roger Cotes FRS, 1682年7月10 –1716年6月5日)著名英國數學家,英國皇家學會會員,他發明了著名的牛頓-柯特斯求和公式(Newton–Cotes formulas),...
數值積分與數值微分 定義 一類重要的求積公式 目錄 1 概念 2 基本原理 ▪ 復化梯形公式 ▪ 復化辛浦生公式 ▪ 復化柯特斯公式 復...
6.2.6牛頓-柯特斯公式求積的算法和程式1746.3復化求積公式1766.3.1問題的提出1766.3.2等距節點復化梯形公式1766.3.3等距節點復化辛普生公式178...
一階牛頓-柯特斯閉型積分公式稱為梯形法則(trapezoidal rule),下面先介紹牛頓-柯特斯公式。梯形法則牛頓-柯特斯公式 牛頓-柯特斯公式(Newton-Cotes formulas)是...
如果n=1,那么牛頓-柯特斯公式就變成梯形公式(取每個小區間兩端點,做成梯形,梯形的值也和矩形一樣,趨於原來的函式的積分)。數值積分高斯型 編輯 一類具有最高的...
5.1 閉牛頓-柯特斯公式2585.2 開牛頓-柯特斯公式和待定係數法2735.3 高斯求積2855.4 高斯-切比雪夫求積2955.5 Radau和洛巴托求積303...
5.2 牛頓-柯特斯公式 5.3 復化求積公式 5.4 龍貝格求積公式 5.5 高斯公式 5.6 數值微分 習題 6 解線性方程組的直接法 6.1 引言 6.2 高斯消...
第三節 牛頓-柯特斯(Newton-Cotes)及其複合求積公式第四節 變步長算法第五節 高斯型求職公式第六節 奇異與振盪積分的計算第七節 二重積分的計算...
4.1.3 插值型的求積公式(100) 4.1.4 求積公式的餘項(101) 4.1.5 求積公式的收斂性與穩定性(102) 4.2 牛頓-柯特斯公式(103) 4.2.1 柯特斯係數與辛普森公...
4.2.2求積公式和它的代數精度 4.2.3插值型的求積公式 4.3牛頓—柯特斯(Newton—Cotes)求積公式 4.3.1公式的推導 4.3.2n低階求積公式的代數精度 4.4龍貝...
3.1.3 插值型求積公式 853.1.4 求積公式的收斂性與穩定性 863.2 牛頓-柯特斯公式及餘項估計 873.2.1 柯特斯係數 873.2.2 偶數階求積公式的代數精度 ...
3.4 Newton(牛頓)插值法3.5 Hermite(艾爾米特)插值法3.6 曲線擬合法第四章 數值積分4.1 引言4.2 數值積分方法4.3 Newten-Cotes(牛頓-柯特斯)求積分公式...
5.4 幾個低次牛頓一柯特斯求積公式5.4.1 矩形求積公式5.4.2 梯形求積公式5.4.3 拋物線求積公式5.4.4 數值積分實例5.5 復化求積公式...
第四章 數值積分與數值微分第一節 牛頓-柯特斯求積公式第二節 復化求積公式第三節 龍貝格求值公式第四節 高斯型求積公式第五節 數值微分習題四第五章 方程求根...
5牛頓法6非線性方程組的數值解法習題第8章數值積分與導數1牛頓—柯特斯公式2牛頓—柯特斯公式的誤差3復化求積公式4變步長復化梯形公式...
3.1.3插值型求積公式 3.1.4求積公式的收斂性與穩定性 3.2牛頓—柯特斯公式及餘項估計 3.2.1柯特斯係數 3.2.2偶數階求積公式的代數精度 3.2.3幾...
2.2.2 牛頓-柯特斯(Newton-Cote's)積分2.3 復化數值積分2.3.1 復化...8.1.3 基於數值積分的差分公式8.2 龍格-庫塔方法8.2.1 二階龍格-庫塔...
8.2 牛頓一柯特斯求積公式 8.2.1 插值型求積方法 8.2.2 梯形求積公式和辛普森求積公式 8.2.3 牛頓一柯特斯公式 8.2.4 代數精確度 8.2.5 偶數階求積...
4.1.3 插值型的求積公式(100)4.1.4 求積公式的餘項(101)4.1.5 求積公式的收斂性與穩定性(102)4.2 牛頓-柯特斯公式(103)4.2.1 柯特斯係數與辛普森公式(...
5.2.4牛頓—柯特斯(Newton—Cotes)求積公式 5.3求積公式拓展 5.3.1龍貝格(Romberg)求積公式 5.3.2數值多重積分 5.4數值微分 5.4.1兩點公式 5.4....
3.2.2牛頓-柯特斯公式 3.2.3龍貝格算法 3.2.4數值微分 3.3方程的求根 3.3.1二分法 3.3.2疊代法 3.3.3牛頓疊代法 3.3.4弦截法 3.4線性方程組...
牛頓柯特斯(NewtonCotes)求積公式150一、 牛頓柯特斯求積公式151 二、 求積公式的代數精確度154三、 求積公式的截斷誤差155 四、 牛頓柯特斯公式的穩定性157五...
2.2 牛頓-柯特斯公式 612.3 龍貝格算法 662.4 高斯公式 712.5 數值微分 76例題選講2.1 機械求積 80例題選講2.2 求積公式的設計 81...
7.3.1 辛普森公式積分方法2347.3.2 辛普森公式的誤差分析2367.4 牛頓-柯特斯公式2387.4.1 牛頓-柯特斯公式積分方法2387.4.2 牛頓-柯特斯公式的誤差分析...
4.2 牛頓—柯特斯公式 4.3 複合型低階牛頓—柯特斯公式 4.3.1 複合求積公式 4.3.2 複合求積公式的誤差 4.4 里查森外推算法與龍貝格積分法 4.4.1 里查...
第21章 牛頓-柯特斯積分公式第22章 函式的積分第23章 數值微分第24章 數值積分和數值微分案例分析第7部分 常微分方程第25章 龍格–庫塔法...
