基本介紹
- 中文名:測度代數
- 外文名:measure algebra
- 所屬學科:數學
- 相關概念:機率空間、保測變換等
基本介紹
定義
測度代數的同構

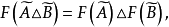
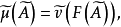
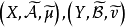
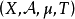
其他介紹

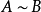
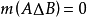




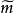
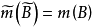
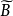
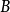
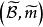
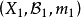
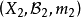
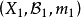
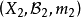
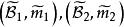
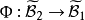
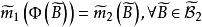
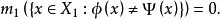


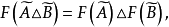
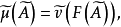
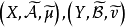
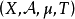

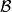
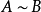
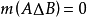




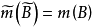
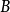
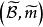
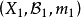
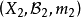
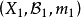
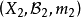
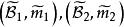
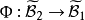
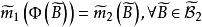
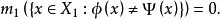
測度代數(measure algebra)定義了正測度的σ代數,若F既是代數又是測度環,則稱F是一個測度代數。若測度μ是有限的或σ有限的,則稱相應的測度代數(測度環)為有限...
若測度μ是σ有限的,則稱相應的測度代數為σ有限的測度代數,又稱為σ有限測度環。...... 若測度μ是σ有限的,則稱相應的測度代數為σ有限的測度代數,又稱為σ...
數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。傳統的積分是在區間上進行的,後來人們希望把積分...
在數學中,某個集合X上的σ代數(σ-algebra)又叫σ域 ,是X的所有子集的集合(也就是冪集)的一個子集。這個子集滿足對於可數個集合的並集運算和補集運算的封閉...
拉東測度是一種正則測度。抽象測度的簡稱,即非負可列可加的集函式,測度論研究的對象。拉東在變分法、實變函式、泛函分析、微分幾何、相對論的數學理論等方面都有...
吉布斯測度(Gibbs measure)是一種常用的測度。數學上,測度是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。...
若測度μ是有限的,則稱相應的測度代數為有限的測度代數,又稱為有限測度環。...... 若測度μ是有限的,則稱相應的測度代數為有限的測度代數,又稱為有限測度環。...
測度論是研究一般集合上的測度和積分的理論。它是勒貝格測度和勒貝格積分理論的進一步抽象和發展,又稱為抽象測度論或抽象積分論,是現代分析數學中重要工具之一。 ...
機率測度(probability measure)是機率論、遍歷理論等數學分支中常用的一種重要的有限測度。在數學中,機率測度是在滿足測度屬性(如可加性)的機率空間中的一組事件上...
代數學基本定理:任何復係數一元n次多項式 方程在複數域上至少有一根(n≥1),由此推出,n次復係數多項式方程在複數域內有且只有n個根(重根按重數計算)。代數基本...
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;...
在數學中,卡爾松測度是對維度歐幾里德空間Rn的子集的一種度量。 Carleson測度以瑞典數學家Lennart Carleson命名。大致來說,域Ω上的Carleson測量是與Ω邊界上的表面...
S測度是超實數集*R中的一種測度,是魯賓孫(Robinson,A.)於20世紀60年代初引入的。...... 測度論是實分析的一個分支,研究對象有σ代數、測度、可測函式和積分,...
正則波萊爾測度(regular Borel measure)是正則的波萊爾測度。設Ω是豪斯多夫空間。如果μ是B(Ω)上的波萊爾測度且是正則的,則稱μ是B(Ω)上的正則波萊爾測度。...
哈爾測度是不恆等於零的不變測度,Rn上的勒貝格測度在拓撲群上的推廣。設G是局部緊豪斯多夫拓撲群,Ω=G,sx(或xs)是群G內的乘法。此時把G上的非零左不變(右...
二元組( X, F),其中F只要滿足三個條件就可以了, 這樣就可以對 F中的元素定義測度, 所以F中的元素叫可測集,但是這時許多人會犯一個致命的錯誤, 認為對 F...
C絕對連續測度(C-absolutely continuous measure)是一種重要的測度。設μ是R上的測度,若對R上的任何α零容的緊集F,都有μ(F)=0,則稱μ為Rn上的C絕對連續...
維納測度是定義在連續函式空間上的一種描述布朗運動的測度。維納測度也叫維納過程。在數學中,維納過程是一個連續的時間隨機過程,以諾伯特·維納命名。它通常被稱為...
σ-有限測度是測度論中的一個概念。給定一個σ-代數,以及其上的一個測度,如果是一個有限的實數(而不是無窮大),那么就稱這個測度為有限測度。...
零測度就是某個集合的測度為0。數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。...
不變測度遍歷分解(ergodic decompositionof invariant measures)反映了不變測度與遍歷不變測度之間的關係.設T為勒貝格空間(X,.},}>上的保測變換,.} (T)表示子...
廣義測度空間,是帶有廣義測度的可測空間,即把可測空間(Ω,𝓕)與其上的廣義測度μ合併在一起來考慮,它就稱為廣義測度空間,記為(Ω,𝓕,μ)。...
布爾代數起源於數學領域,是一個用於集合運算和邏輯運算的公式:〈B,∨,∧,¬ 〉。其中B為一個非空集合,∨,∧為定義在B上的兩個二元運算,¬為定義在B上的...
茹利亞集測度(measure of Julia set)是關於沒有內點的茹利亞集的測度問題。人們知道,茹利亞集非空。當茹利亞集有內點時,它必為整個平面。一個有趣的問題是:...
《91國優教材:泛函分析講義(下冊)》一部泛函分析教材,它系統地介紹線性運算元理論的基礎知識,運算元半群以及連續函式空間上的Wiener測度和Hilbert空間上的Gauss測度。全書...
根據柯爾莫哥洛夫機率測度存在性定理,在φ的代數對偶空間φA(φ上的線性泛函全體)上存在σ 代數B和機率測度μ,使得φA上的由φ(ƒ)=ƒ(φ)(φ∈φ,ƒ...
可測變換(可測函式)又稱為可測映射,是從一個測度空間到另一個測度空間之間的一個映射,它將前者中的可測集映射為後者中的可測集。可測變換在測度論是十分重要...
