保測變換(measure-preserving transformation)是遍歷性理論研究的基本變換,代表一個系統的保持某種信息量的隨時間的演化。
基本介紹
- 中文名:保測變換
- 外文名:measure preserving transformation
- 所屬學科:數學
- 性質:遍歷性理論研究的基本變換
- 相關概念:影射、可測影射、龐加萊定理等
定義






保測變換舉例
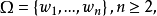



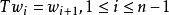


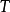
保測變換的物理前提條件



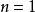
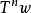



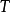
關於保測變換的龐加萊定理








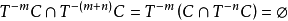
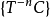

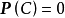

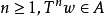
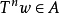

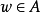
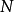
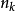
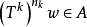
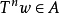
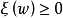
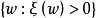
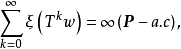
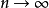
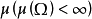
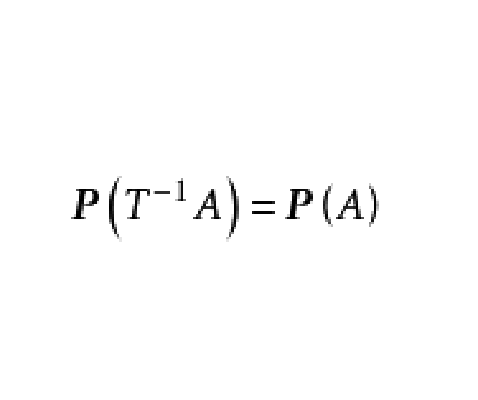
保測變換(measure-preserving transformation)是遍歷性理論研究的基本變換,代表一個系統的保持某種信息量的隨時間的演化。






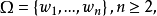



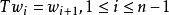





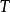
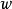

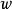


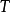



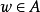

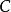




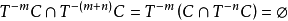
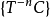

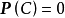

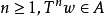
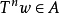

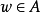
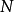
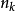
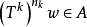
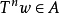
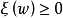
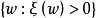
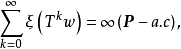
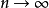
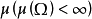
保測變換(measure-preserving transformation)遍歷性理論研究的基本變換,代表一個系統的保持某種信息量的隨時間的演化...
保測變換共軛(conjugacy of measure-pre-serving transformations)是保測變換分類的一種方法。...
保測變換同構(isomorphism of measure-pre-serving transformations)保測變換之I旬的一種等價關係.遍歷論的一個重要研究課題就是保測變換的分類問題。...
度量可遞性質(保測變換或平穩序列的)(metrically transitive property (of measure-preserving transformation or stationary sequence))是一種與遍歷性有密切關係的...
保測動力系統(Measure-preserving dynamical system)一個保測動力系統定義為一個機率空間和其上的一個保測變換. ...
遍歷理論是研究保測變換的漸近性態的數學分支。它起源於為統計力學提供基礎的"遍歷假設"研究,並與動力系統理論、機率論、資訊理論、泛函分析、數論等數學分支有著密切...
則稱兩個測度代數 是同構的,對保測系統 ,令設 分別為 上的保測變換,若存在同構 ,使 ,則稱T和S是共軛的。容易證明,同構⇒共軛⇒譜同構,但反之未必成立...
5.7.1 相空間上的保測變換5.7.2 Boltzmann 遍歷假設5.7.3 不可壓縮穩定流5.7.4 遍歷定理5.7.5 變換群的遍歷性習題第六章 無窮維空間的微分學...
