基本介紹
定義,數學性質,本徵值和向量,泡利向量,對易關係,內積外積關係,指數,完備性關係,和換位符關係,SU (2),
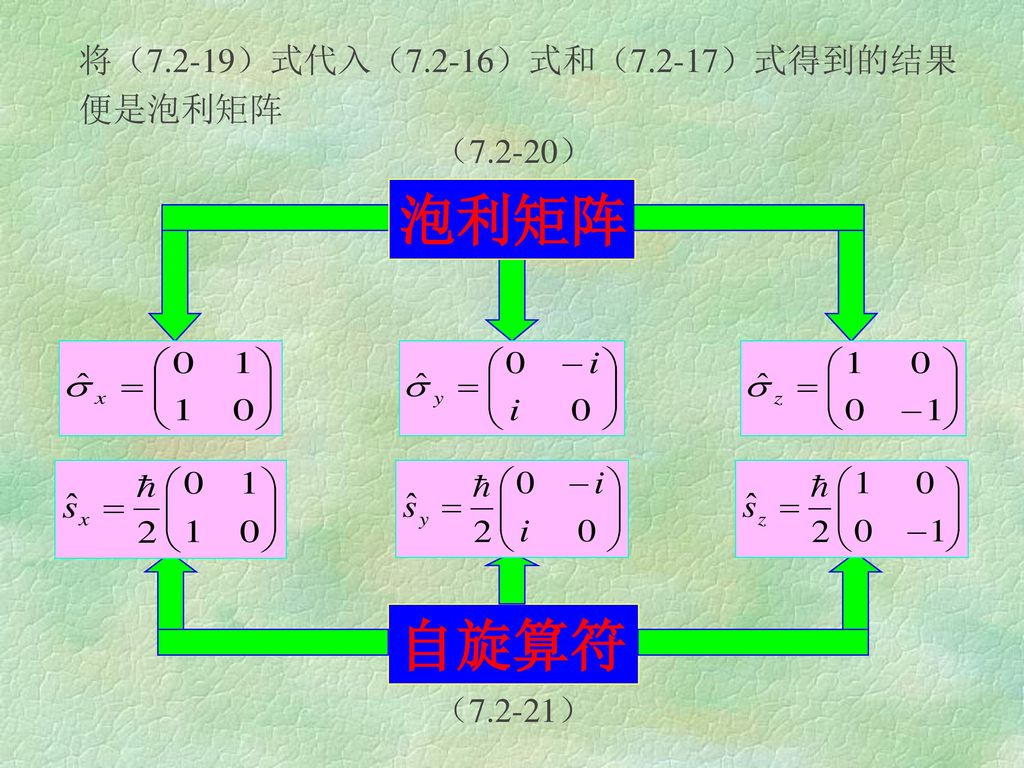
定義



這些矩陣是以物理學家沃爾夫岡·泡利命名的。在量子力學中,它們出現在泡利方程中描述磁場和自旋之間相互作用的一項。所有的泡利矩陣都是厄米矩陣,它們和單位矩陣I(有時候又被稱為為第零號泡利矩陣σ0),的線性張成為2×2厄米矩陣的向量空間。
從量子力學的角度來看,哈密頓矩陣(算符)代表可觀測的物理量,因此,σk,k= 0,1,2,3的線性張成代表所有作用在二維希爾伯特空間的物理量所形成的空間。從泡利本人的的研究來看,σk,k=1,2,3所代表的物理量是自旋在三維歐幾里得空間ℝ中第k個坐標軸的投影分量。
數學性質
三個泡利矩陣可以共同用一種單一形式表達:

其中δab是克羅內克δ函式。當a=b時,其值為1;當a≠b時,其值為0。
本徵值和向量
這些矩陣是對合的:
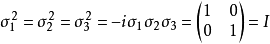
其中I是單位矩陣。


故從上述關係可以推得每個泡利矩陣σi的本徵值分別為±1。
每個泡利矩陣有兩個本徵值,+1和−1,其對應的歸一化本徵向量為:

泡利向量
包向量定義為:


對易關係
泡利矩陣有以下的對易關係:

以及以下的反對易關係。

其中εabc是列維-奇維塔符號,δab是克羅內克函式,是I是2 ×2的單位矩陣。而一樣的,上面使用了愛因斯坦求和約定。
內積外積關係
將泡利矩陣的對易和反對易相加得:


因此可得:

為了避免符號重複,將a,b,c改成p,q,r,然後把上式和三維向量ap和bq內積,可得:


將它轉換成向量積的表達式:

指數
令 ,而且
,而且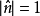 對於偶數n可得:
對於偶數n可得: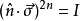

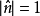
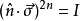
另外加上之前求得在n= 1的情況可在n為基數的情況:

利用矩陣指數的概念,加上正弦和餘弦的泰勒級數展開式,可得:
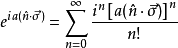
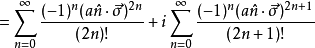

第一項的總和為 ,第二項括弧里的總和是
,第二項括弧里的總和是 ,於是:
,於是: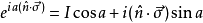


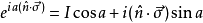
這可以看做是歐拉公式的類比。
完備性關係
另一個常用來區別泡利矩陣的方法是用上標i,用不同的i來代表不同的泡利矩陣,而下標則代表不同的矩陣元素。因此第i個泡利矩陣的第α行第β列的元素可表示為σαβ
利用這種表示方法,泡利矩陣的完備性關係可寫作:

證明
因為所有的泡利矩陣,和2×2的單位矩陣可做為所有2×2矩陣在希爾伯特空間中的正交基底,表示任何一個復係數矩陣M皆可表示為: 其中c是一複數,ai是一復向量中的三個係數。
其中c是一複數,ai是一復向量中的三個係數。

利用之前給的關係式,容易證明:

故,

用矩陣的標號表示的話就成為:

在等號右邊,針對了兩個重複出現的標號γ和δ,使用了愛因斯坦求和約定。而因為這關係對所有矩陣M都成立,因此要證的完備性關係必然成立。
有時習慣上將2×2單位舉寫成σ0,也就是,σαβ=δαβ。如此一來完備性關係可以更為簡潔的表示成:

和換位符關係
令算符Pij為換位算符(或稱為置換算符)。對於兩個在張量積空間ℂ⊗ ℂ中的自旋σi和σj該算符有:
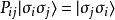
的關係。這個算符可以更進一步的用泡利矩陣來表示:

SU (2)
四元數與泡利矩陣

另外一種方式的映射為將泡利矩陣的次序反轉

既然單位四元數與SU(2)為群同構,此亦代表泡利矩陣也可用來描述SU(2)。從SU(2)到SO(3)的2對1同態性,也可以用泡利矩陣來表述。