群表示是處理分子振動、價鍵理論和晶體場理論問題中的一種強有力工具。正交定理是構成群的不可約表示矩陣元的一個基本定理。這個定理揭示出用群來描述一個系統的結構細節。
基本介紹
- 中文名:正交定理
- 外文名:orthogonality theorem
- 定義:構成群的不可約表示矩陣元
- 套用學科:量子力學術語
- 範疇:理工科
- 涉及:群
概念
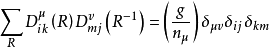
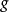
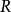
基本原理
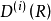
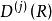
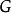

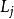
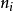
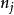
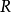
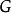
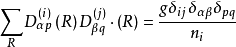
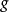
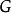
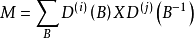
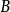
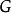
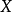
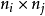
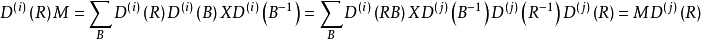
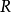
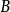
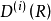
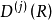
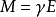
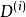
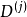
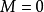
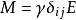

群表示是處理分子振動、價鍵理論和晶體場理論問題中的一種強有力工具。正交定理是構成群的不可約表示矩陣元的一個基本定理。這個定理揭示出用群來描述一個系統的結構細節。
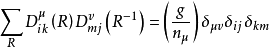
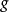
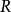
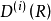
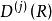
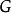

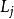
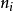
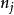
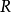
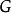
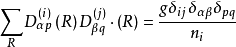
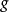
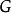
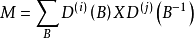
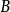
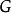
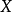
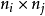
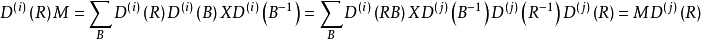
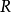
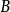
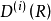
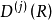
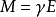
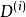
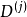
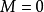
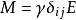
群表示是處理分子振動、價鍵理論和晶體場理論問題中的一種強有力工具。正交定理是構成群的不可約表示矩陣元的一個基本定理。這個定理揭示出用群來描述一個系統的...
正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域。...... (Gram—Schmidt)正交化程式構造出標準正交向量組,在內積空間中則有下述的定理...
“正交向量”是一個數學術語,指點積為零的兩個或多個向量。幾何向量的概念線上性代數中經由抽象化,得到更一般的向量概念。此處向量定義為向量空間的元素,要注意...
施密特正交化(Schmidt orthogonalization)是求歐氏空間正交基的一種方法。從歐氏空間任意線性無關的向量組α1,α2,……,αm出發,求得正交向量組β1,β2,……,...
舒爾正交關係(Schur orthogonality relations)描述了有限群表示中的核心事實。它可以推廣到一般的緊群,特別是緊李群,比如旋轉群 SO(3)。此關係可藉由舒爾引理證明。...
如果AAT=E(E為單位矩陣,AT表示“矩陣A的轉置矩陣”)或ATA=E,則n階實矩陣A稱為正交矩陣。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。儘管我們在這裡...
正交分解法是:求合力的一種方法。就是將受力物體所受外力平移到平面坐標系的原點(限同一平面內的共點力)並沿選定的相互垂直的x軸和y軸方向分解,然後分別求出...
規範正交基(orthonormal basis)完備的規範正交系。設H為希爾伯特空間,H的完備的規範正交系F稱為H的規範正交基或正規正交基。F的基數稱為希爾伯特空間H的維數。兩...
正交陣列(orthogonal array)是一類組合設計,設A是v元集X上的v×k矩陣,若對任意d(2≤d≤k)列所構成的子矩陣,X上的每一個d元排列作為子矩陣的行各出現λ次...
Π-定理,即量綱分析基本原理,是量綱分析法的理論基礎。這個定理由Backingham在1914年提出。到了1922年,R.W.Bridgman把這個定理稱為Π定理, 這是因為π這個符號是...
定義:(飽和正交拉丁方組)設S 是 n 階正交拉丁方組,若 |S|=n-1,則稱 S 是飽和的。3. 定理: 若 n 是素數方冪,則存在飽和的 n 階正交拉丁方組。...
平面上的一個點變換(點變成點的變換),如果保持點之間的距離不變,則稱它為正交變換(或等距變換),正交變換具有眾多性質,比如正交變換的乘積是正交變換,恆等變換是...
在數學中,帕塞瓦爾定理經常指“傅立葉轉換是么正算符”這一結論;簡而言之,就是說函式平方的和(或積分)等於其傅立葉轉換式平方之和(或者積分)。這個定理產生於...
如果向量空間被賦予了內積,那么就可以定義正交和其它相關的概念(比如線性運算元的自...通過哈恩-巴拿赫定理,存在一個有界線性泛函φ,使得φ(u)=1。運算元P(x)=φ(...
達朗貝爾定理是關於變換的著名定理。該定理斷言:每個有不動點的空間第一種契約變換是一個空間旋轉。達朗貝爾在微分方程、力學兩方面貢獻都很大。1743年出版了他的著作...
這個定理建立了希爾伯特空間與它的對偶空間的一個重要聯繫:如果底域是實數,兩者是等距同構;如果域是複數,兩者是等距反同構。在泛函分析中有多個有名的定理冠以里斯...
希爾伯特一施密特定理(Hilbert-Schmidt theo-em)對稱核積分方程的主要定理.設k(二,勻是對 稱核,^7 f ^2 f " .. f } f…是齊次積分方程x)一、{:*(x,...
科克倫定理是科克倫於1934年提出的定理。獨立正態隨機變數的線性函式仍然服從正態變數,但是,獨立正態隨機變數的二次型函式與χ2分布有著密切的聯繫,科克倫定理...
嘉當-迪奧多內定理是數學中以埃利·嘉當與讓·迪厄多內命名的定理,此定理所涉及的是對稱雙線性形式的自同構群。...
“華氏定理”是我國著名數學家華羅庚的研究成果。 華氏定理為:體的半自同構必是自同構自同體或反同體。 數學家華羅庚關於完整三角和的研究成果被國際數學界稱為“...
數學定理列表(按字母順序排列)以下列出了許多數學定理,供查閱與引用。...... 以下列出了許多數學定理,供查閱與引用。中文...哥德爾不完備定理割線定理廣義正交定理...
里斯-費希爾定理是貝塞爾不等式的逆命題。貝塞爾不等式表明:{ck}為L2[a,b]中某個函式的傅立葉係數的必要條件是{ck}2的和函式收斂,里斯-費希爾定理表明這個條件...
在數論中,狄利克雷定理說明對於任意互質的正整數a,d,有無限多個質數的形式如a+nd,其中n為正整數,即在等差數列a+d,a+2d,a+3d,...中有無限多個質數——...
弗雷德霍姆定理(Fredholm theorems)積分方程的基本定理.設第二類弗雷德霍姆積分方程是稱為方程(1)的轉置方程。...
