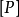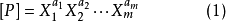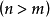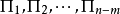Π-定理,即量綱分析基本原理,是量綱分析法的理論基礎。這個定理由Backingham在1914年提出。到了1922年,R.W.Bridgman把這個定理稱為Π定理, 這是因為π這個符號是由Buckingham在定理的推導和證明中用來表示無量綱量的緣故。關於量綱的套用,除了一般的介紹單位的換算、檢查公式的對錯等少數方面,但量綱分析法有是量綱分析的理論核心。
| 中文名稱 | Π-定理 |
| 英文名稱 | Πtheorem |
| 定 義 | 任何一個由n個有量綱的物理量參與的物理過程中的函式關係都可以轉換成由n-k個這些物理量組成的無量綱量Πi之間的函式關係,其中k是具有獨立量綱的物理量的數。由於這些無量綱量是以不同的Πi數來表示的,故稱為Π定理。 |
| 套用學科 | 航空科技(一級學科),飛行原理(二級學科) |
基本介紹
定理內容,量綱,Π定理,證明,等價形式,套用,量子漲落,勾股定理,
定理內容
量綱
由於各物理量之間存在規律性的聯繫,我們不必對每個物理量的單位都獨立地予以規定。我們可以選取一些物理量作為“基本量”,並且為每個基本量規定一個“基本量度單位”,其他物理量的量度單位則可以按照它們與基本量之間的關係式(定義或定律)導出,這些物理量稱為“導出量”,它們的單位稱為“導出單位”。按照此種方法構成的一套單位,構成一定的“單位制”。在不同的單位制中,不僅基本量的選取可以不同,基本量的數目也可以不同。例如,CGS單位制中有三個基本量,MKSA單位制中有四個基本量。
量綱可以看成是某個“矢量空間”中的“矢量”。於是,對 式兩端取對數,則有
式兩端取對數,則有


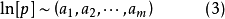





Π定理
量綱分析法的理論基礎是Π-定理,這個定理是E.Buckingham在1914年提出的:

可相應表達為無量綱形式:
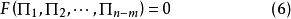
(在m= 的情況下有兩種可能:若
的情況下有兩種可能:若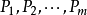 的量綱彼此獨立,則不能由他們組成無量綱的量;若不獨立,則還可能組成無量綱的量。)
的量綱彼此獨立,則不能由他們組成無量綱的量;若不獨立,則還可能組成無量綱的量。)

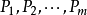
證明
設 個物理量的量綱為
個物理量的量綱為

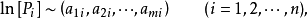




寫成分量形式,用矩陣表示,則有:

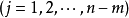
由於等式左端方陣的行列式不等於零,故對每個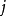 有一組解
有一組解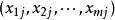 ,共
,共 組,這就是說,我們有
組,這就是說,我們有
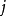
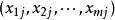

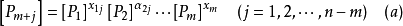


我們構想把 的量度單位分別改變為原來的
的量度單位分別改變為原來的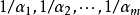 ,則在這個單位制下這些量的數值
,則在這個單位制下這些量的數值 與原來的數值
與原來的數值 有如下關係:
有如下關係:

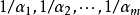




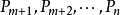





函式式 不應該受度量單位變化的影響,亦即我們有:
不應該受度量單位變化的影響,亦即我們有:


對於上述的特殊選擇,有


等價形式
Π定理可以表示為另一等價形式,這一形式在很多場合更便於使用。在一定問題中物體系的發展和演化往往由若干個變數決定,不妨叫做“主定參量”在上面的推演中, 實際上起著一組新基矢的作用,我們盡可以選為代表主定參量的量綱矢量。如果在其他的物理量中我們感興趣的是其中的某一個,譬如
實際上起著一組新基矢的作用,我們盡可以選為代表主定參量的量綱矢量。如果在其他的物理量中我們感興趣的是其中的某一個,譬如 ,則我們可以從
,則我們可以從 式中把
式中把 解出來:
解出來:





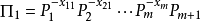

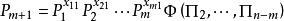
套用
Π-定理有許多套用,給出兩個例子。
量子漲落
構想兩塊無限大平面壁相距 ,皆由理想導體構成。從經典理論看,兩壁之間應該沒有作用力。,但若計及(相對論性)電磁場的量子真空漲落效應,求兩壁單位面積上的作用力
,皆由理想導體構成。從經典理論看,兩壁之間應該沒有作用力。,但若計及(相對論性)電磁場的量子真空漲落效應,求兩壁單位面積上的作用力 也即壓強和距離
也即壓強和距離 的函式關係。
的函式關係。



利用Π-定理解答是。除了距離 外,這裡涉及電磁場,有關的參量為真空中的光速
外,這裡涉及電磁場,有關的參量為真空中的光速 ;還涉及到量子效應,有關的參量還有普朗克常數
;還涉及到量子效應,有關的參量還有普朗克常數 ,從量綱表
,從量綱表




可以解出 ,即
,即

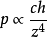


勾股定理
這個著名的定理,又稱畢達哥拉斯定理,也可以用量綱法來證明。
一個直角三角形的面積可由它的一邊(譬如斜邊 )和一個銳角(譬如
)和一個銳角(譬如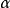 )決定。
)決定。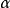 是無量綱的,根據定理的等價形式,可以寫出:
是無量綱的,根據定理的等價形式,可以寫出:

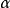
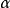
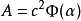

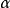


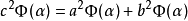

這便是勾股定理。