基本介紹
- 中文名:次導數
- 外文名:subderivative
- 適用範圍:數理科學
定義


例子
性質
- 凸函式f:I→R在x0可導,若且唯若次微分只由一個點組成,這個點就是函式在x0的導數。
- 點x0是凸函式f的最小值,若且唯若次微分中包含零,也就是說,在上面的圖中,我們可以作一條水平的“次切線”。這個性質是“可導函式在極小值的導數是零”的事實的推廣。
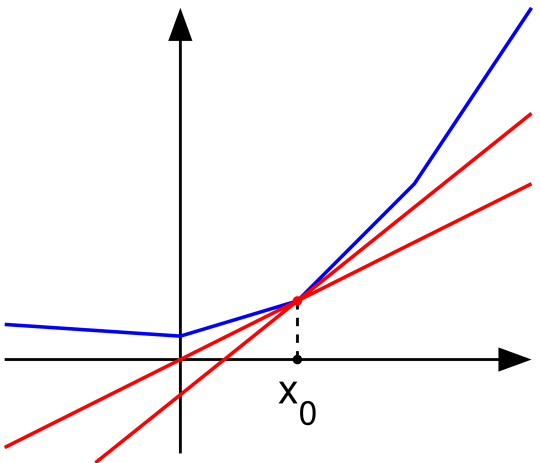


次導數、次切線和次微分的概念出現在凸分析,也就是凸函式的研究中。設f:I→R是一個實變數凸函式,定義在實數軸上的開區間內。這種函式不一定是處處可導的,...
二階導數,是原函式導數的導數,將原函式進行二次求導。一般的,函式y=f(x)的導數yˊ=fˊ(x)仍然是x的函式,則y′′=f′′(x)的導數叫做函式y=f(x)的二...
三階導數是由原函式導數的導數的導數。...... 所謂三階導數,即原函式導數的導數的導數,將原函式進行三次求導,不代表該點的曲率,談幾何意義頂多只能算代表原函式...
一階導數的導數稱為二階導數,二階以上的導數可由歸納法逐階定義。二階和二階以上的導數統稱為高階導數。從概念上講,高階導數可由一階導數的運算規則逐階計算,...
重力位二階導數(second derivative of gravity potential)是重力場強度(g)在空間單位距離上的變化...
化極△T垂向一階導數就是在化極的基礎上,求磁場沿垂直方向一次一次變換率的數據轉換處理。垂向一次導數處理對磁場高頻成分有突出和放大作用,它側重於淺層近地表...
次導數(subderivative)、次微分(subdifferential)、次切線(subtangent lines)和次梯度(subgradient)的概念出現在凸分析,也就是凸函式的研究中。 要注意的是,次切線...
重力高次倒數法,別名重力垂向二階導數,所屬科目數學。...... 重力高次倒數法,別名重力垂向二階導數,所屬科目數學。中文名 重力高次倒數法 外文名 無 別名 ...
在數學和計算機代數中,自動微分有時稱作演算式微分,是一種可以藉由電腦程式計算一個函式導數的方法。兩種傳統做微分的方法為:(1)對一個函式的表示式做符號上的...
數值微分是數值方法中的名詞,是用函式的值及其他已知資訊來估計一函式導數的算法。根據函式在一些離散點的函式值,推算它在某點的導數或某高階導數的近似值。通常...
若函式f(x)在開區間(a,b)有直到n+1階的導數,則當函式在此區間內時,可以展開為一個關於x多項式和一個餘項的和:Tauc公式:其中Rn是公式的餘項,可以是如下:...
