基本介紹
- 中文名:柯爾莫哥洛夫檢驗
- 外文名:Kolmogolov test
- 領域:統計學
- 提出者:柯爾莫哥洛夫
- 提出時間:1933
- 套用:檢驗完全已知的連續型分布函式
定義
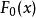
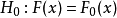
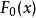
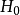


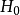
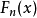
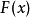
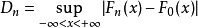
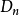

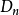

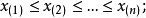


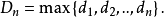


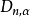
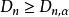

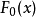

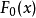




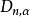
正態性檢驗
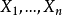
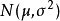
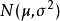
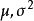
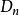
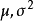
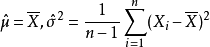
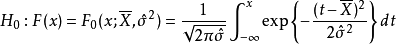

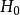
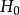

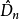
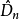


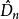
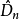
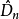
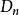
指數分布的檢驗

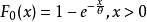

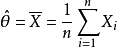
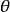

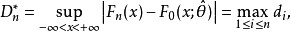
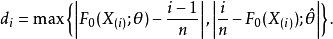


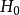


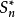

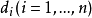

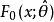
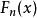
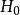


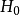
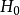
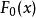
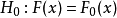
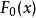
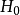


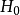
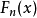
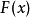
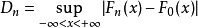
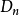

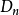

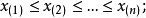


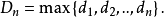


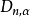
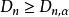

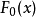

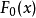




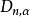
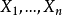
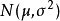
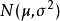
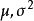
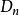
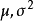
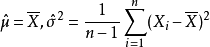
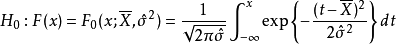

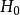
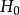

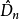
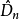


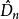
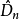
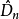
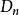

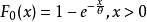

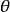

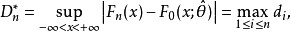
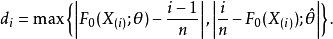





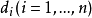

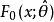
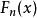
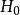


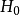
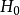
柯爾莫哥洛夫檢驗是由柯爾莫哥洛夫提出的一種分布擬合檢驗,用於檢驗完全已知的連續型分布函式。...
斯米爾諾夫檢驗是斯米爾諾夫藉助於經驗分布函式給出了與柯爾莫哥洛夫檢驗相類似的檢驗統計量,都要求總體分布函式是連續的。斯米爾諾夫檢驗精確度高,計算也比較簡便。....
柯爾莫哥洛夫定理是關於Lp[a,b]的子集為列緊集的特徵的定理。...... 柯爾莫哥洛夫定理是關於Lp[a,b]的子集為列緊集的特徵的定理。 [1] ...
柯爾莫哥洛夫檢驗(見非參數統計)也是一個重要的擬合優度檢驗方法。奈曼-皮爾森理論 J.奈曼與 E.S.皮爾森合作,從1928年開始,對假設檢驗提出了一項系統的理論。...
柯爾莫哥洛夫理論(Kolmogorov theory)即局部均勻各向同性湍流,是由柯爾莫哥洛夫於1941年在建立湍流的統計理論過程中提出的三個基本假設。...
柯爾莫哥洛夫特徵是最佳逼近元的一種特徵刻畫。倘若G不是X的線性子空間,則結論未必成立。...
查普曼一柯爾莫哥洛夫方程是馬爾可夫過程理論中用來刻畫轉移機率特性的一組方程。...... 查普曼一柯爾莫哥洛夫方程是馬爾可夫過程理論中用來刻畫轉移機率特性的一組方程...
費希爾-柯爾莫哥洛夫方程是羅納德·費希爾和安德雷·柯爾莫哥洛夫命名的非線性偏微分方程...
安德列·柯爾莫哥洛夫(1903年4月25日-1987年10月20日),20世紀蘇聯最傑出的數學家,也是20世紀世界上為數極少的幾個最有影響的數學家之一。他的研究幾乎遍及...
柯爾莫哥洛夫前向方程是群體遺傳學中研究基因頻率變化的一個方程。...... 柯爾莫哥洛夫前向方程是群體遺傳學中研究基因頻率變化的一個方程。中文名 柯爾莫哥洛夫...
柯爾莫哥洛夫相容性定理(Kolmogorov consis-tency theorem)在無窮維空間上構造機率測度的定理.如果一個機率分布函式族 成立,則在(R 0" , },x})上存在機率測度...
檢測理論是20世紀40年代二次大戰中與估計理論同時發展起來的。初創階段,N.維納和A.H.柯爾莫哥洛夫等作出了傑出貢獻。他們把隨機過程和數理統計方法引入到通信和...
柯爾莫哥洛夫微分方程是連續時間參數馬爾可夫鏈理論中的兩組微分方程.首先由蘇聯數學家俄國數學家柯爾莫哥洛夫(}OJIMOPOpOB } A. H.)推出。...
柯爾莫哥洛夫後向方程是群體遺傳學中研究基因頻率變化的一個方程。...... 柯爾莫哥洛夫後向方程是群體遺傳學中研究基因頻率變化的一個方程。中文名 柯爾莫哥洛夫...
柯爾莫哥洛夫不等式(Kolmogorov inequality)是次線性運算元是弱型的一種不等式刻畫。...... 柯爾莫哥洛夫不等式(Kolmogorov inequality)是次線性運算元是弱型的一種不...
德雷·柯爾莫哥洛夫(俄語:Андре́й Никола́евичКолмого́ров,1903年4月25日-1987年10月20日),俄國數學家,主要在...
柯爾莫哥洛夫強大數律(Kolmogorov strong law of large numbers)是最重要最常用的強大數律。若{Xn}為獨立同分布隨機變數序列,EXn存在,則以機率1成立n個獨立同...
柯爾莫哥洛夫熵(Kolmogorov熵,以下簡稱K熵)是刻劃混沌系統的一個重要的量。在不同類型的動力學系統中,K熵的數值是不同的。...
柯爾莫哥洛夫,為機率論建立了公理體系的蘇聯數學家。...... 柯爾莫哥洛夫建立了在測度論基礎上的機率論公理系統,奠定了近代機率論的基礎,他也是隨機過程論的奠基...
常用的非參數檢驗有:基於實際觀測頻數與理論期望頻數差異的皮爾遜檢驗;基於經驗分布函式和理論分布函式或兩經驗分布函式之差的柯爾莫哥洛夫一斯米爾諾夫檢驗等。 [1]...
總體分布為某一個或某一類具體分布Fo(x;B)的各種檢驗法的總稱.最常用的擬合良好J勝檢驗有Xz擬合良好性檢驗.柯爾莫哥洛夫檢驗等.這些檢驗法都屬於非參數檢驗....
《鐵礦石檢驗結果的數據處理》是2009年冶金工業出版社出版的圖書,作者是任春生。...2.5.2 X擬合優度檢驗法2.5.3 柯爾莫哥洛夫擬合檢驗——Dn檢驗...
柯爾莫哥洛夫考察 Fn(x)與理論分布F(x)的最大偏差墹n,當墹n超過一定限度時,否定這個理論分布F(x)。這就是柯爾莫哥洛夫檢驗。斯米爾諾夫則考察由兩個分布為...
這就是柯爾莫哥洛夫檢驗。斯米爾諾夫則考慮由兩個分布為F(x)和G(x)的總體中抽出的樣本X1,X2…,Xm和Y1,Y2,…,Yn,計算其經驗分布Fm(x)和Gn(x)的最大...
Kolmogorov-Smirnova,柯爾莫哥洛夫,斯米爾諾夫D試驗或堪薩斯州Lilliefors試驗 ,大樣本的選擇是一個正常的檢驗。...
1.3.1 X2檢驗1.3.2 柯爾莫哥洛夫檢驗1.3.3 常態分配的其它檢驗方法第2章 維修性的度量和試驗樣本2.1 維修性的基本概念2.1.1 維修性的定量描述...
12.4.2 皮爾遜χ 2檢驗 12.4.3 最小二乘、極大似然估計中的皮爾遜χ 2檢驗 12.4.4 擬合優度的一般χ 2檢驗 12.4.5 柯爾莫哥洛夫檢驗 12.4....
