柯爾莫哥洛夫微分方程是連續時間參數馬爾可夫鏈理論中的兩組微分方程.首先由蘇聯數學家俄國數學家柯爾莫哥洛夫(}OJIMOPOpOB } A. H.)推出。

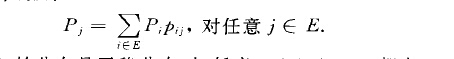
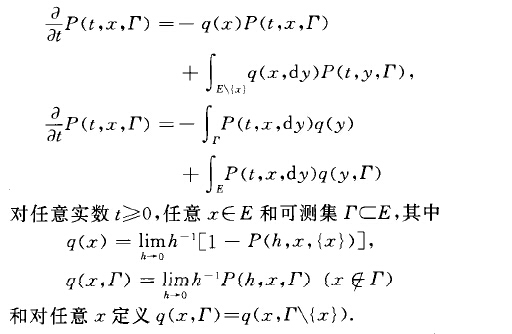
柯爾莫哥洛夫微分方程是連續時間參數馬爾可夫鏈理論中的兩組微分方程.首先由蘇聯數學家俄國數學家柯爾莫哥洛夫(}OJIMOPOpOB } A. H.)推出。

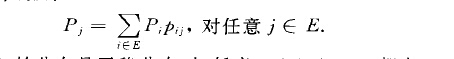
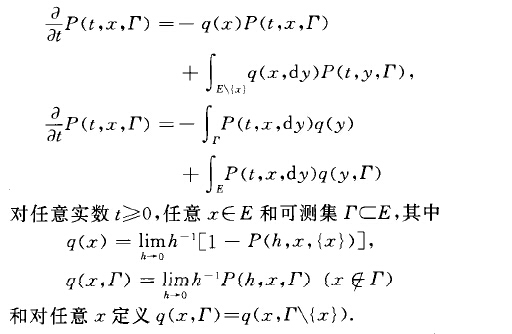
柯爾莫哥洛夫微分方程是連續時間參數馬爾可夫鏈理論中的兩組微分方程.首先由蘇聯數學家俄國數學家柯爾莫哥洛夫(}OJIMOPOpOB } A. H.)推出。...
費希爾-柯爾莫哥洛夫方程是羅納德·費希爾和安德雷·柯爾莫哥洛夫命名的非線性偏微分方程...
安德列·柯爾莫哥洛夫(1903年4月25日-1987年10月20日),20世紀蘇聯最傑出的數學家,也是20世紀世界上為數極少的幾個最有影響的數學家之一。他的研究幾乎遍及...
概周期微分方程的發展歷史不長,但由於它具有實際背景(如天體力學和非線性振動的問題)而顯示出生命力。特別是,1945年,A.H.柯爾莫哥洛夫利用無理性條件,指出哈密...
德雷·柯爾莫哥洛夫(俄語:Андре́й Никола́евичКолмого́ров,1903年4月25日-1987年10月20日),俄國數學家,主要在...
非線性偏微分方程的在物理學、氣動力學、流體力學、大氣物理、海洋物理、爆炸...Fisher-Kolmogorov 費希爾-柯爾莫哥洛夫方程 :: Fujita-Storm 藤田-斯托姆方程...
安德列·柯爾莫哥洛夫(1903年4月25日-1987年10月20日),20世紀蘇聯最傑出的數學家,也是20世紀世界上為數極少的幾個最有影響的數學家之一。他的研究幾乎遍及...
積分方程即為關於未知函式Φ (x) 的積分方程。許多微分方程的求解問題可以歸結...考慮非均勻流體中懸浮晶粒的布朗位移和熱擴散,導致了以柯爾莫哥洛夫命名的一類...
關於馬爾可夫過程的理論研究,1931年Α.Η.柯爾莫哥洛夫發表了《機率論的解析方法》,首先將微分方程等分析方法用於這類過程,奠定了它的理論基礎。1951年前後,伊藤清...
柯爾莫哥洛夫發現了吉米多維奇對微分方程的興趣,於是邀請他一道同斯捷潘諾夫教授研究微分方程的定性理論。1935年獲副博士學位,後成為莫斯科大學數學分析教研室教授,在...
2.6 隨機微分方程2.7 習題第3章 馬爾可夫鏈3.1 馬爾可夫鏈3.2 切普曼一柯爾莫哥洛夫方程3.2.1 切普曼一柯爾莫哥洛夫方程3.2.2 初始機率分布及絕對機率...
由柯爾莫哥洛夫和杜布奠定目錄 1 基本簡介 2 隨機過程的研究 ▪ 研究方法...中國學者在平穩過程、馬爾可夫過程、鞅論、極限定理、隨機微分方程等方面也做出了...
第四節 馬爾可夫鏈的套用 第五節 連續時間馬爾可夫鏈 第六節 轉移機率和柯爾莫哥洛夫微分方程 習題 第六章 鞅 ……詞條標籤: 文化, 出版物 圖集...
費希爾-柯爾莫哥洛夫方程是以英國統計學家羅納德·費希爾和俄國數學家安德雷·柯爾莫哥洛夫命名的非線性偏微分方程。...
關於該過程的研究,1931年A.H.柯爾莫哥洛夫在《機率論的解析方法》一文中首先將微分方程等分析的方法用於這類過程,奠定了馬爾可夫過程的理論基礎。1951年前後,伊藤...
5.2柯爾莫哥洛夫費勒(Kolmogrov Feller)微分方程5.3生滅過程5.4馬爾可夫序列與擴散過程5.5套用舉例第6章鞅和布朗運動6.1鞅的基本概念和性質...
莫澤在發展柯爾莫哥洛夫一阿譜爾德一莫澤 (KAM)理論中起了重要作用,該理論...還證明了橢圓與拋物型微分方程中的哈納克不等 式,現已成為非線性偏微分方程中...
第六節 轉移機率和柯爾莫哥洛夫微分方程習題第六章 鞅第一節 基本概念第二節 鞅的停時定理及一個套用第三節 一致可積性第四節 鞅收斂定理...
