查普曼一柯爾莫哥洛夫方程是馬爾可夫過程理論中用來刻畫轉移機率特性的一組方程。
查普曼一柯爾莫哥洛夫方程(Chapman-Kolmo-gorov equations)馬爾可夫過程理論中用來刻畫轉移機率特性的一組方程.對於一般的非齊次馬爾可夫過程,查普曼一柯爾莫哥洛夫方程是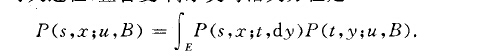
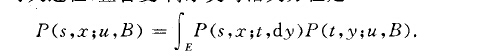
其中、,t,“是滿足0簇、簇t簇u的任意實數,B是狀態空間E的任意可測集,P(s,x,u,B)是過程的轉移機率。即當已知過程在時刻、處於狀態x時,它在時刻u將轉移到集合B中的條件機率.對於齊次馬爾可夫過程,這組方程為
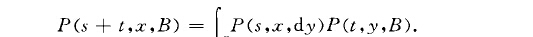
其中、,t是任意非負實數,B的意義同上,P<t,y,B>是轉移機率.即當已知過程在初始時刻處於狀態y}經過長為t的時間後將轉移到集合B中的條件機率.在馬爾可夫鏈的情形中,對應的查普曼一柯爾莫哥洛夫方程要用離散求和代替積分(參見“轉移機率矩陣”).
