從哈密頓原理可以等價地推出相應的質點組的運動方程,通常是微分方程。如果力學系統處於靜力平衡穩定狀態,則因動能為零,位能與時間無關,哈密頓原理轉化為最小位能原理。
基本介紹
- 中文名:最小位能原理
- 外文名:least potential energy principle
- 適用範圍:數理科學
簡介
哈密頓原理
定義
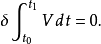
套用
彈性理論中的最小位能原理
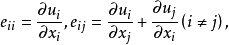
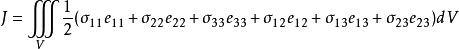
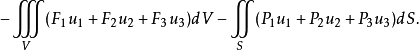
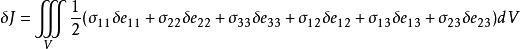
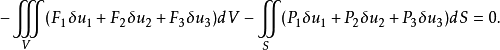
從哈密頓原理可以等價地推出相應的質點組的運動方程,通常是微分方程。如果力學系統處於靜力平衡穩定狀態,則因動能為零,位能與時間無關,哈密頓原理轉化為最小位能原理。
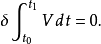
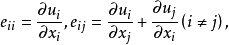
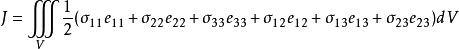
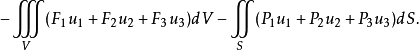
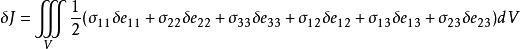
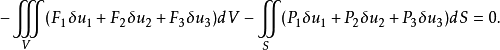
從哈密頓原理可以等價地推出相應的質點組的運動方程,通常是微分方程。如果力學系統處於靜力平衡穩定狀態,則因動能為零,位能與時間無關,哈密頓原理轉化為最小位能...
最小勢能原理屬物理學範疇,是指當一個體系的勢能最小時,系統會處於穩定平衡狀態。舉個例子來說,一個小球在曲面上運動,當到達曲面的最低點位置時,系統就會趨向於...
在物理學裡,最小作用原理,即最小作用量原理(英語:least action principle),或更精確地,平穩作用量原理(英語:stationary action principle),是一種變分原理,當套用...
最小作用量原理(principle of least action):是物理學中描述客觀事物規律的一種方法。即從一個角度比較客體一切可能的運動(經歷),認為客體的實際運動(經歷)可以由...
當一體系處於平衡態時,體系的自由能最小,據此可以確定體系中穩定的相、各相的組成及各相相對的量。...
彈性力學最小余能原理是彈性力學的能量原理之一,最小余能原理實質上等價於彈性體的變形連續條件。它可作為彈性力學直接解法和有限元法計算的重要基礎。...
彈性力學最小勢能原理是彈性力學的能量原理之一,它可作為彈性力學直接解法和有限元計算的重要基礎。...
最小相位頻移鍵控MSK的基本原理 編輯 最小相位頻移鍵控是2FSK(二進制頻移鍵控)的一種特殊情況,具有正交信號的最小頻差,在相領符號交界處信號的相位保持連續...
能位匹配原理,也即能位原理,是指人力資源管理管理人員應根據員工的才能,把員工安排到相應的崗位上,從而保證崗位的需求和員工的能力相匹配。...
最小二乘法原理 編輯 在我們研究兩個變數(x,y)之間的相互關係時,通常可以得到一系列成對的數據(x1,y1.x2,y2... xm,ym);將這些數據描繪在x -y直角坐標...
最小運費原理是在生產過程不可分割、消費地和局地原料產地都只有一個的前提下,以產生最小運費為目標的區位指向。...
