基本介紹
- 中文名：旅行商問題
- 外文名：Traveling Salesman Problem
- 簡稱：TSP
- 又稱：貨郎擔問題
- 提出者：Dantzig
- 提出時間：1959年
簡介,研究歷史,分類,經典TSP,不對稱TSP,配送收集TSP,多人旅行商問題,多目標旅行商問題,問題解法,解法思路,途程建構法,途程改善法,研究進展,問題分析,枚舉法,回溯法,分支限界法,貪心法,套用,
簡介
旅行商問題(TravelingSalesmanProblem，TSP)是一個經典的組合最佳化問題。經典的TSP可以描述為：一個商品推銷員要去若干個城市推銷商品，該推銷員從一個城市出發，需要經過所有城市後，回到出發地。應如何選擇行進路線，以使總的行程最短。從圖論的角度來看，該問題實質是在一個帶權完全無向圖中，找一個權值最小的Hamilton迴路。由於該問題的可行解是所有頂點的全排列，隨著頂點數的增加，會產生組合爆炸，它是一個NP完全問題。由於其在交通運輸、電路板線路設計以及物流配送等領域內有著廣泛的套用，國內外學者對其進行了大量的研究。早期的研究者使用精確算法求解該問題，常用的方法包括：分枝定界法、線性規劃法、動態規劃法等。但是，隨著問題規模的增大，精確算法將變得無能為力，因此，在後來的研究中，國內外學者重點使用近似算法或啟發式算法，主要有遺傳算法、模擬退火法、蟻群算法、禁忌搜尋算法、貪婪算法和神經網路等。
研究歷史
TSP的研究歷史很久，最早的描述是1759年歐拉研究的騎士環遊問題，即對於西洋棋棋盤中的64個方格，走訪64個方格一次且僅一次，並且最終返回到起始點。1954年，Geo~eDanzig等人用線性規劃的方法取得了旅行商問題的歷史性的突破——解決了美國49個城市的巡迴問題。這就是割平面法，這種方法在整數規劃問題上也廣泛套用。後來還提出了一種方法叫做分枝限界法，所謂限界，就是求出問題解的上、下界，通過當前得到的限界值排除一些次優解，為最終獲得最優解提示方向。每次搜尋下界最小的分枝，可以減小計算量。
分類
經典TSP
CTSP是在一個帶權無向完全圖中找一個權值最小的Hamilton迴路。在各類TSP中，該類問題的研究成果最多。近幾年來，研究者或者基於數學理論構造近似算法，或者使用各種仿自然的算法框架結合不同的局部搜尋方法構造混合算法。同時，神經網路和自組織圖方法在該問題上的套用研究也引起了研究者的關注。
不對稱TSP
若在CTSP模型中，兩個頂點i和j間的距離d不一定相等，則稱為 ATSP。ATSP由於兩點間距離的不對稱性，所以求解更困難，但由於現實生活中多數實際場景都為不對稱的TSP，所以對於基於實際交通網路的物流配送來說，其比CTSP更具有實際套用價值 。
配送收集TSP
TSPPD是由CTSP適應物流配送領域的實際需求而產生的。這個問題涉及到兩類顧客需要：一類是配送需求，要求將貨物從配送中心送到需求點；另一類是收集需求，要求將貨物從需求點運往配送中心。當所有的配送和收集需求都由一輛從配送中心出發、限定容量的車輛來完成時，怎樣安排行駛路線才能構成一條行程最短的 Hamilton迴路。
多人旅行商問題
即多個旅行商遍歷多個城市，在滿足每個城市被一個旅行商經過一次的前提下，求遍歷全部城市的最短路徑。解決 MTSP對解決 “車輛調度路徑安排 ”問題具有重要意義。過去的研究大多將 MTSP轉化成多個TSP，再使用求解 TSP的算法進行求解。Hong Qu等人結合勝者全取 (winner—take—all)的競爭機制設計了一個柱形競爭的神經網路模型來求解MTSP，並對網路收斂於可行解進行了分析和論證。
多目標旅行商問題
CRISP的路徑上只有一個權值 (即距離)，而 MoTSP研究的是路徑上有多個權值的 TSP，要求找一條通過所有頂點並最終回到起點的迴路，使迴路上的各個權值都儘可能小。由於在多目標情況下，嚴格最優解並不存在，研究 MoTSP的目的是找到Pareto最優解，這是一個解集，而不是一個單一解。現階段算法為構造一個求解單目標的遺傳局部搜尋算法，然後基於此求解多目標組合最佳化問題算法。
問題解法
旅行推銷員的問題，我們稱之為巡行（Tour），此種問題屬於NP完全問題，所以旅行商問題大多集中在啟發式解法。Bodin（1983）等人將旅行推銷員問題的啟發式解法分成三種：
1、途程建構法（TourConstructionProcedures）
從距離矩陣中產生一個近似最佳解的途徑，有以下幾種解法：
1）最近鄰點法（NearestNeighborProcedure）：一開始以尋找離場站最近的需求點為起始路線的第一個顧客，此後尋找離最後加入路線的顧客最近的需求點，直到最後。
2）節省法（ClarkandWrightSaving）：以服務每一個節點為起始解，根據三角不等式兩邊之和大於第三邊之性質，其起始狀況為每服務一個顧客後便回場站，而後計算路線間合併節省量，將節省量以降序排序而依次合併路線，直到最後。
3）插入法（Insertion procedures）：如最近插入法、最省插入法、隨意插入法、最遠插入法、最大角度插入法等。
2、途程改善法（TourImprovementProcedure）
先給定一個可行途程，然後進行改善，一直到不能改善為止。有以下幾種解法：
1）K-Opt(2/3Opt)：把尚未加入路徑的K條節線暫時取代目前路徑中K條節線，並計算其成本（或距離），如果成本降低（距離減少），則取代之，直到無法改善為止，K通常為2或3。
2）Or-Opt：在相同路徑上相鄰的需求點，將之和本身或其它路徑交換且仍保持路徑方向性，並計算其成本（或距離），如果成本降低（距離減少），則取代之，直到無法改善為止。
3、合成啟發法（CompositeProcedure）
先由途程建構法產生起始途程，然後再使用途程改善法去尋求最佳解，又稱為兩段解法（twophasemethod）。有以下幾種解法：
1）起始解求解+2-Opt：以途程建構法建立一個起始的解，再用2-Opt的方式改善途程，直到不能改善為止。
2）起始解求解+3-Opt：以途程建構法建立一個起始的解，再用3-Opt的方式改善途程，直到不能改善為止。
蜜蜂試驗解法思路
旅行推銷員的問題，我們稱之為巡行（Tour），此種問題屬於NP完全問題（NP-Complete），所以旅行商問題大多集中在啟發式解法。Bodin（1983）等人將旅行推銷員問題的啟發式解法分成三種：
途程建構法
算法的核心從距離矩陣中產生一個近似最佳解的途徑，有以下幾種解法：
1、近鄰點法（Nearest Neighbor Procedure）：一開始以尋找離場站最近的需求點為起始路線的第一個顧客，此後尋找離最後加入路線的顧客最近的需求點，直到最後。
2、節省法（ClarkandWright Saving）：以服務每一個節點為起始解，根據三角不等式兩邊之和大於第三邊之性質，其起始狀況為每服務一個顧客後便回場站，而後計算路線間合併節省量，將節省量以降序排序而依次合併路線，直到最後。
3、插入法（Insertion procedures）：如插入法、最省插入法、隨意插入法、最遠插入法、最大角度插入法等。
途程改善法
先給定一個可行途程，然後進行改善，一直到不能改善為止。有以下幾種解法：
1、K-Opt(2/3Opt)：把尚未加入路徑的K條節線暫時取代如今路徑中K條節線，並計算其成本（或距離），如果成本降低（距離減少），則取代之，直到無法改善為止，K通常為2或3。
2、Or-Opt：在相同路徑上相鄰的需求點，將之和本身或其它路徑交換且仍保持路徑方向性，合成啟發法
先由途程建構法產生起始途程，然後再使用途程改善法去尋求最佳解，又稱為兩段解法（twophasemethod）。有以下幾種解法：
1、起始解求解+2-Opt：以途程建構法建立一個起始的解，再用2-Opt的方式改善途程，直到不能改善為止。
2、起始解求解+3-Opt：以途程建構法建立一個起始的解，再用3-Opt的方式改善途程，直到不能改善為止。
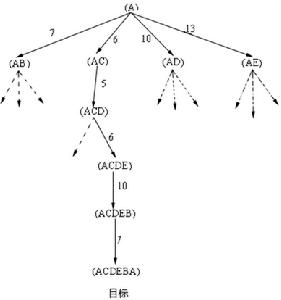
研究進展
2010年10月25日，英國一項最新研究說，在花叢中飛來飛去的小蜜蜂顯示出了輕易破解“旅行商問題”的能力，而這是一個吸引全世界數學家研究多年的大問題，如能理解蜜蜂的解決方式，將有助於人們改善交通規劃和物流等領域的工作。英國倫敦大學皇家霍洛韋學院等機構研究人員報告說，小蜜蜂顯示出了輕而易舉破解這個問題的能力。他們利用人工控制的假花進行了實驗，結果顯示，不管怎樣改變花的位置，蜜蜂在稍加探索後，很快就可以找到在不同花朵間飛行的最短路徑。這是首次發現能解決這個問題的動物，研究報告即將發表在《美國博物學家》雜誌上。
小蜜蜂解決大問題
小蜜蜂解決大問題進行研究的奈傑爾·雷恩博士說，蜜蜂每天都要在蜂巢和花朵間飛來飛去，為了采蜜而在不同花朵間飛行是一件很耗精力的事情，因此實際上蜜蜂每天都在解決“旅行商問題”。儘管蜜蜂的大腦只有草籽那么大，也沒有電腦的幫助，但它已經進化出了一套很好的解決方案，如果能理解蜜蜂怎樣做到這一點，對人類的生產、生活將有很大幫助。
據介紹，“旅行商問題”的套用領域包括：如何規劃最合理高效的道路交通，以減少擁堵；如何更好地規劃物流，以減少運營成本；在網際網路環境中如何更好地設定節點，以更好地讓信息流動等。
問題分析
旅行商問題要從圖G的所有週遊路線中求取最小成本的週遊路線，而從初始點出發的週遊路線一共有(n-1)!條，即等於除初始結點外的n-1個結點的排列數，因此旅行商問題是一個排列問題。通過枚舉(n-1)!條週遊路線，從中找出一條具有最小成本的週遊路線的算法，其計算時間顯然為O(n!)。
枚舉法
程式中採用深度優先策略。（採用隱式和顯式兩種形式）
枚舉算法的特點是算法簡單，但運算量大，當問題的規模變大，循環的階數越大，執行的速度越慢。如果枚舉範圍太大（一般以不超過兩百萬次為限），在時間上就難以承受。在解決旅行商問題時，以頂點1為起點和終點，然後求{2…N}的一個全排列，使路程1→{2…N}的一個全排列→1上所有邊的權（代價）之和最小。所有可能解由（2，3，4，…，N）的不同排列決定。
為便於討論，介紹一些關於解空間樹結構的術語。在下面分析回溯法和分支限界法時都直接或間接用到解空間樹。在解空間樹中的每一個結點確定所求問題的一個問題狀態（problem state）。由根結點到其它結點的所有路徑則確定了這個問題的狀態空間（state space）。解狀態（solution states）表示一些問題狀態S，對於這些問題狀態，由根到S的那條路徑確定了這解空間中的一個元組。答案狀態（answer states）表示一些解狀態S，對於這些解狀態而言，由根到S的這條路徑確定了這問題的一個解（即，它滿足隱式約束條件）。解空間的樹結構稱為狀態空間樹（state pace tree）。
對於旅行商問題，一旦構想出一種狀態空間樹，那么就可以先系統地生成問題狀態，接著確定這些問題狀態中的哪些狀態是解狀態，最後確定哪些解狀態是答案狀態，從而將問題解出。為了生成問題狀態，採用兩種根本不同的方法。如果已生成一個結點而它的所有兒子結點還沒有全部生成，則這個結點叫做活結點。當前正在生成其兒子結點的活結點叫E-結點。不再進一步擴展或者其兒子結點已全部生成的生成結點就是死結點。在生成問題狀態的兩種方法中，都要用一張活結點表。在第一種方法中，當前的E-結點R一旦生成一個新的兒子C，這個兒子結點就變成一個新的E-結點，當完全檢測了子樹C之後，R結點就再次成為E-結點。這相當與問題狀態的深度優先生成。在第二種狀態生成方法中，一個E-結點一直保持到死結點為止。這兩種方法中，將用限界函式去殺死還沒有全部生成其兒子結點的那些活結點。如果旅行商問題要求找出全部解，則要生成所有的答案結點。使用限界函式的深度優先結點生成方法稱為回溯法。E-結點一直保持到死為止的狀態生成方法稱為分支限界法。
回溯法
為了套用回溯法，所要求的解必須能表示成一個n-元組(x1,…,Xn)，其中x1是取自某個有窮集Si。通常，所求解的問題需要求取一個使某一規範函式P(x1,…,Xn)取極大值（或取極小值或滿足該規範函式條件）的向量。
分支限界法
採用FIFO分支限界法，分支限界法是在生成當前E-結點全部兒子之後再生成其它活結點的兒子，且用限界函式幫助避免生成不包含答案結點子樹的狀態空間的檢索方法。在總的原則下，根據對狀態空間樹中結點檢索的次序的不同又將分支限界設計策路分為數種不同的檢索方法。在求解旅行商問題時，程式中採用FIFO檢索（First In First Out），它的活結點表採用一張先進先出表（即佇列）。可以看出，分支限界法在兩個方面加速了算法的搜尋速度，一是選擇要擴展的節點時，總是選擇選擇一個最小成本的結點，儘可能早的進入最有可能成為最優解的分支；二是擴展節點的過程中，捨棄導致不可行解或導致非最優解的子結點。
貪心法
貪心法是一種改進了的分級處理方法。它首先旅行商問題描述，選取一種度量標準。然後按這種度量標準對n個輸入城市排序，並按序一次輸入一個城市。如果這個輸入和當前已構成在這種量度意義下的部分最優解加在一起不能產生一個可行解，則不把這個城市加入到這部分解中。這種能夠得到某種量度意義下的最優解的分級處理方法成為貪心方法。
獲得最優路徑的貪心法應一條邊一條邊地構造這棵樹。根據某種量度來選擇將要計入的下一條邊。最簡單的量度標準是選擇使得迄今為止計入的那些邊的成本的和有最小增量的那條邊。
套用
旅行商問題具有重要的實際意義和工程背景。它一開始是為交通運輸而提出的，比如飛機航線安排、送郵件、快遞服務、設計校車行進路線等等。實際上其套用範圍擴展到了許多其他領域．下面舉幾個實例。
印製電路板轉孔是TSP套用的經典例子，在一塊電路板上打成百上千個孔，轉頭在這些孔之間移動，相當於對所有的孔進行一次巡遊。把這個問題轉化為TSP，孔相當於城市．孔到孔之問的移動時間就是距離。
為了避免大氣干擾，使光學系統達到其衍射極限解析度．歐美已開發國家提出發展空間光干涉儀和綜合孔徑望遠鏡的計畫。美國航空航天局有一個衛星群組成空間天文台(Space—basedObservatories)的計畫，用來探測宇宙起源和外星智慧生命。歐洲空間局也有類似的Darwin計畫。對天體成像的時候，需要對兩顆衛星的位置進行調整，如何控制衛星，使消耗的燃料最少，可以用TSP來求解。這裡把天體看作城市，距離就是衛星移動消耗的燃料。
美國國家衛生協會在人類基因排序工作中用TSP方法繪製放射性雜交圖。把DNA片段作為城市．它們之間的相似程度作為城市間的距離。法國科學家已經用這種辦法作出了老鼠的放射性雜交圖。
