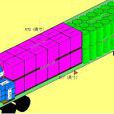
基本介紹
- 中文名：裝箱問題
- 外文名：bin-packing problem
- 別名：組合最佳化問題
- 分類：一二三維
- 一維：重量，體積，長度
- 三維問題：箱櫃裝載問題，容器裝載問題
- 二維：面積問題
簡介,定義,分類,按照裝箱物體所屬裝箱空間,按照裝箱物體的形狀,按照裝箱物體達到情況,解決辦法,數學規劃法(Mathematieal Programming),構造法(Construetion Algorithms),數值最佳化方法(optimal Algorithms),現代最佳化方法,
簡介
從20世紀70年代初開始,裝箱問題就引起了廣泛的探討和研究。然而裝箱問題可以追溯到1831年高斯(Gauss)開始研究布局問題，因為裝箱問題和布局問題本質上是一樣的,到現在已有百餘年的歷史。雖然經過幾代人的努力,但迄今尚無成熟的理論和有效的數值計算方法。由於目前NP完全問題不存在有效時間內求得精確解的算法,裝箱問題的求解極為困難,因此,從70~80年代開始,陸續提出的裝箱算法都是各種近似算法,如下次適應、首次適應、降序下次適應和調和算法等。
裝箱問題廣泛存在於工業生產,包括服裝行業的面料裁剪、運輸行業的貨櫃貨物裝載、加工行業的板材型材下料、印刷行業的排樣和現實生活中包裝、整理物件等。在計算機科學中,多處理器任務調度、資源分配、檔案分配、記憶體管理等底層操作均是裝箱問題的實際套用,甚至還出現在一些棋盤形、方塊形的數學智力遊戲中。裝箱問題的研究文獻分布面很廣,在運籌學、計算機輔助設計、計算機圖形學、人工智慧、圖像處理、大規模積體電路邏輯布線設計、計算機套用科學等諸多領域都有裝箱問題最新的研究動態和成果出現,從這個角度來講,布局問題涉及到了工業生產的方方面面,也足以證明了裝箱問題的套用前景日趨廣泛而重要。
定義
設有許多具有同樣結構和負荷的箱子 B1，B2，… ，其數量足夠供所達到
目的之用。每個箱子的負荷（可為長度、重量等等.）為 C ，今有 n 個負荷為 wj，0 < wj < C ， j = 1，2，…，n 的物品 J1，J2，…，Jn 需要裝入箱內。裝箱問題就是指尋找一種方法，使得能以最小數量的箱子數將J1，J2，…，Jn 全部裝入箱內。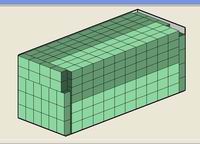
裝箱問題
裝箱問題分類
按照裝箱物體所屬裝箱空間
二維裝箱問題考慮兩個因素——給定一張矩形的紙（布料、皮革），要求從這張紙上剪出給定的大小不一的形狀，求一種剪法使得剪出的廢料的面積總和最小。常見問題包括堆場中考慮長和寬進行各功能區域劃分、停車場區位劃分、包裝材料裁切時考慮怎樣裁切使得材料浪費最少、服裝布料裁切、皮鞋製作中的皮革裁切等。
三維裝箱問題考慮三個因素——一般指長、寬、高。裝車、裝船、裝貨櫃等要考慮這三個維度都不能超。
根據目標的不同,三維裝箱問題可分成以下幾類：
箱櫃裝載問題(three-dimensional bin packing problem，簡稱3D-BPP)：給定一些不同類型的方型箱子和一些規格統一的方型容器，問題是要把所有箱子裝入最少數量的容器中。
容器裝載問題(three-dimensional container-packing problems，簡稱3D-CPP)：在該問題中，所有箱子要裝入一個不限尺寸的容器中，目標是要找一個裝填，使得容器體積最小。
背包裝載問題(three-dimensional knapsack loading problems，簡稱3D-KLP)：每個箱子有一定的價值，背包裝載是選擇一部分箱子裝入容器中，使得裝入容器中的箱子總價值最大。如果把箱子的體積作為價值，則目標轉化為使容器浪費的體積最小。
按照裝箱物體的形狀
1).規則物體的裝箱
包括二維規則物體的裝載和三維規則物體的裝載。規則物體是指具有規則外形的物體,例如圓柱體、矩形體等。在以前及現在的裝載研究中,研究較多的仍然是規則體的裝載問題,如:工業套用中的底盤裝載;三維布局中的貨櫃的貨物擺放問題。
貨物底盤裝載問題廣泛存在於工業生產和交通運輸中。由於箱子的大小和形狀完全相同,且箱子的邊平行於底盤的邊,因此該問題也可簡化為二維問題。對於該問題,有的學者使用精確的方法求解。在運輸生產中,常見的貨櫃裝載要求有兩類,一是貨櫃數量無限,而待裝的貨物有限,要使貨櫃利用率最高;二是貨櫃數量固定,待裝貨物數量無限,遠遠超過己有貨櫃的承載能力,一般是其幾倍,要求在有限的貨櫃空間內儘可能地多裝貨物,使貨櫃利用率最高,生產實際中更多地遇到的是第2類問題。貨櫃布局要考慮貨物重量、空間利用率、貨物易碎性、以及吊裝的可能性等等,為多目標多約束最佳化問題。
2).不規則物體的裝箱
包括二維不規則物體的裝載和三維不規則物體的裝載。不規則物體是指具有任意幾何形狀的物體。不規則物體的裝箱問題在工業生產中大量存在,但同時也是難度最大的裝箱問題。二維不規則物體的裝箱如服裝樣本的下料、皮革下料等。三維不規則物體的裝箱如向具有任意幾何形狀的容器中放置任意幾何外形的裝箱物體,並滿足特定的約束條件,達到裝箱目標最優。該問題的求解算法基本上是啟發式的。
按照裝箱物體達到情況
1).線上裝箱問題
如果一個裝箱算法在裝入物品時，只利用前面物品的信息，而不知道後繼元素的任何信息，即按照元素到達順序隨到隨裝，則稱該算法為線上(online)算法。這種情況下的裝箱問題稱為線上裝箱問題。在實際套用中，往往要求裝載具有線上特性。例如對從傳送帶上下來的物體進行裝載。
2).離線裝箱問題
物品裝載以前就已得到所有物品信息,之後統一處理所有物品的近似算法稱為離線(offline)裝箱算法。這種情況下的裝箱問題稱為離線裝箱問題。現代化的物流配送中,很多都要求按訂單送貨,因此物品的信息提前都是知道的。該問題廣泛地出現在鐵路貨車車廂裝載、汽車車廂裝載、輪船配載、貨櫃裝載等情況中。
解決辦法
數學規劃法(Mathematieal Programming)
數學規劃法包括分枝定界法(Braneh一and一boundAlgorithm)、動態規劃法(Dynamieprogr~ing)、整數規劃法(Integerprograunning)和線性規劃法(Linearprogramming)等。該方法利用某一最佳化問題的數學模型,通過修改該模型的精確求解過程得到有效的啟發式算法。這四種方法中分枝定界法套用較廣泛。該方法的基本思想是試圖通過枚舉解空間中的有限個解來獲得NP完全問題的局部最優解。它由分枝和定界兩個操作步驟組成,分枝操作用於將規模較大的原始問題逐步分解為規模較小且易於求解的子問題;而定界操作主要用於評價各分枝的優劣,來減小搜尋範圍。二維切割問題中,“一刀切”問題是該方法的經典套用,如玻璃切割、紙張裁剪等。
構造法(Construetion Algorithms)
裝箱啟發式算法中使用最多的方法是構造性算法。構造啟發式算法通過一個一個地增加解的構造元素來求得一個可行解。構造性算法的循環次數與問題解的構造元素個數成正比,而與解空間的大小無關,因此其計算速度通常很快。
裝箱問題中構造法基本上由兩類規則組成。第一類為定序規則(orderingrules),它被用來確定待布局物體放入布局空間的先後順序:第二類為定位規則(Placement rules),它用來確定每一個布局物體在布局空間擺放的位置。由於定序規則和定位規則的不同,也就產生不同的構造布局方法。常用的定序規則有: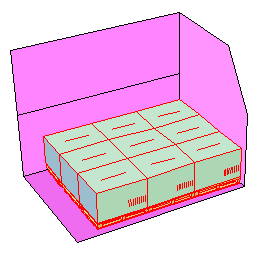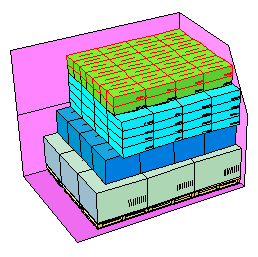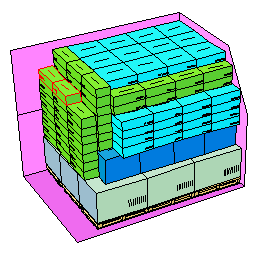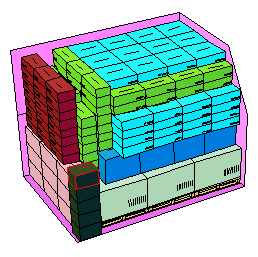
裝箱問題求解
裝箱問題求解(l)按照待裝物體最短邊邊長遞減的順序進行定序:
(2)按照待裝物體最長邊邊長遞減的順序進行定序;
(3)按照待裝物體體積遞減的順序進行定序;
(4)按照待裝物體最小面積遞減的順序進行定序;
(5)按照待裝物體可行域遞減的順序進行定序:
許多學者對布局問題中定位規則進行了研究,提出了如下一些規則和策略:
(1)占角策略,即將待裝物體擺放在布局容器的某一角:
(2)順放策略,即從布局容器的某一角開始將待裝物體沿著容器某一邊擺放;
(3)在底盤裝載中,將待裝物體先沿著邊放置,最後擺放到底盤中心;
(4)在三維規則裝箱中,從布局容器的某一面牆開始,一層一層地布局;在某一面牆上,再確定一條邊,最後歸結為一個角:
(5)在三維規則裝箱中,先按“右、前、上”的順序找尋剩餘空間,然後按照“左、後、下”的順序擺待裝局物體:
數值最佳化方法(optimal Algorithms)
數值最佳化方法具有較為成熟的理論和算法,廣泛套用於工程設計領域；取得了許多有效成果,裝箱問題是它的一個套用分支,但是數值最佳化方法依賴於數學模型,且只能找到局部最優解,它只適用於小規模物體的裝箱問題。對於規模大的裝箱問題用數學模型很難準確描述,即使能用簡化的數學模型來描述,由於局部最優解數目的急劇增加,其求解質量也將嚴重變壞。此外,數值最佳化方法所得解的質量在很大程度上還依賴於初始解的選擇。
