NP完全問題

NP完全問題(NP-C問題)，是世界七大數學難題之一。 NP的英文全稱是Non-deterministic Polynomial的問題，即多項式複雜程度的非確定性問題。簡單的寫法是 NP=P？，問題就在這個問號上，到底是NP等於P，還是NP不等於P。

基本介紹

• 中文名：NP完全問題
• 外文名：Non-deterministic Polynomial
• 屬性：世界七大數學難題之一
• 解釋：多項式複雜程度的非確定性問題
• 縮寫：NPC

詳細信息

P類問題：所有可以在多項式時間內求解的判定問題構成P類問題。判定問題：判斷是否有一種能夠解決某一類問題的能行算法的研究課題。

NP類問題：所有的非確定性多項式時間可解的判定問題構成NP類問題。非確定性算法：非確定性算法將問題分解成猜測和驗證兩個階段。算法的猜測階段是非確定性的，算法的驗證階段是確定性的，它驗證猜測階段給出解的正確性。設算法A是解一個判定問題Q的非確定性算法，如果A的驗證階段能在多項式時間內完成，則稱A是一個多項式時間非確定性算法。有些計算問題是確定性的，例如加減乘除，只要按照公式推導，按部就班一步步來，就可以得到結果。但是，有些問題是無法按部就班直接地計算出來。比如，找大質數的問題。有沒有一個公式能推出下一個質數是多少呢？這種問題的答案，是無法直接計算得到的，只能通過間接的“猜算”來得到結果。這也就是非確定性問題。而這些問題的通常有個算法，它不能直接告訴你答案是什麼，但可以告訴你，某個可能的結果是正確的答案還是錯誤的。這個可以告訴你“猜算”的答案正確與否的算法，假如可以在多項式（polynomial）時間內算出來，就叫做多項式非確定性問題。

NPC問題：NP中的某些問題的複雜性與整個類的複雜性相關聯.這些問題中任何一個如果存在多項式時間的算法,那么所有NP問題都是多項式時間可解的.這些問題被稱為NP-完全問題(NPC問題)。

舉例敘述

在一個周六的晚上，你參加了一個盛大的晚會。由於感到局促不安，你想知道這一大廳中是否有你已經認識的人。你的主人向你提議說，你一定認識那位正在甜點盤附近角落的女士羅絲。不費一秒鐘，你就能向那裡掃視，並且發現你的主人是正確的。然而，如果沒有這樣的暗示，你就必須環顧整個大廳，一個個地審視每一個人，看是否有你認識的人。

生成問題的一個解通常比驗證一個給定的解時間花費要多得多。這是這種一般現象的一個例子。與此類似的是，如果某人告訴你，數13,717,421可以寫成兩個較小的數的乘積，你可能不知道是否應該相信他，但是如果他告訴你他可以因式分解為3607乘上3803，那么你就可以用一個袖珍計算器容易驗證這是對的。人們發現，所有的完全多項式非確定性問題，都可以轉換為一類叫做滿足性問題的邏輯運算問題。既然這類問題的所有可能答案，都可以在多項式時間內計算，人們於是就猜想，是否這類問題，存在一個確定性算法，可以在多項式時間內，直接算出或是搜尋出正確的答案呢？這就是著名的NP=P？的猜想。 不管我們編寫程式是否靈巧，判定一個答案是可以很快利用內部知識來驗證，還是沒有這樣的提示而需要花費大量時間來求解，被看作邏輯和計算機科學中最突出的問題之一。它是斯蒂文·考克於1971年陳述的。

千僖難題

背景

美國麻州的克雷（Clay）數學研究所於2000年5月24日在巴黎法蘭西學院宣布了一件被媒體炒得火熱的大事：對七個“千僖年數學難題”的每一個懸賞一百萬美元。

內容

“千僖難題”之一：P （確定性多項式算法）對NP （非確定性多項式算法）

“千僖難題”之二：霍奇（Hodge）猜想

“千僖難題”之三：龐加萊（Poincare）猜想

“千僖難題”之四：黎曼（Riemann）假設

“千僖難題”之五：楊－米爾斯（Yang-Mills）存在性和質量缺口

“千僖難題”之六：納維葉－斯托克斯（Navier-Stokes）方程的存在性與光滑性

“千僖難題”之七：貝赫（Birch）和斯維訥通－戴爾（Swinnerton-Dyer）猜想

評價

NP完全問題排在百萬美元大獎的首位，足見他的顯赫地位和無窮魅力。

簡介

NP就是Non-deterministic Polynomial的問題，也即是多項式複雜程度的非確定性問題。而如果任何一個NP問題都能通過一個多項式時間算法轉換為某個NP問題，那么這個NP問題就稱為NP完全問題（Non-deterministic Polynomial complete problem）。NP完全問題也叫做NPC問題。

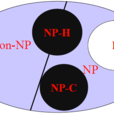
假設P ≠ NP的圖解。若P = NP則三類相同。

有些計算問題是確定性的，比如加減乘除之類，你只要按照公式推導，按部就班一步步來，就可以得到結果。但是，有些問題是無法按部就班直接地計算出來。比如，找大質數的問題。有沒有一個公式，你一套公式，就可以一步步推算出來，下一個質數應該是多少呢？這樣的公式是沒有的。再比如，大的合數分解質因數的問題，有沒有一個公式，把合數代進去，就直接可以算出，它的因子各自是多少？也沒有這樣的公式。

這種問題的答案，是無法直接計算得到的，只能通過間接的“猜算”來得到結果。這就是非確定性問題。而這些問題的通常有個算法，它不能直接告訴你答案是什麼，但可以告訴你，某個可能的結果是正確的答案還是錯誤的。這個可以告訴你“猜算”的答案正確與否的算法，假如可以在多項式時間內算出來，就叫做多項式非確定性問題。而如果這個問題的所有可能答案，都是可以在多項式時間內進行正確與否的驗算的話，就叫完全多項式非確定問題。

完全多項式非確定性問題可以用窮舉法得到答案，一個個檢驗下去，最終便能得到結果。但是這樣算法的複雜程度，是指數關係，因此計算的時間隨問題的複雜程度成指數的增長，很快便變得不可計算了。

人們發現，所有的完全多項式非確定性問題，都可以轉換為一類叫做滿足性問題的邏輯運算問題。既然這類問題的所有可能答案，都可以在多項式時間內計算，人們於是就猜想，是否這類問題存在一個確定性算法，可以在多項式時間內直接算出或是搜尋出正確的答案呢？這就是著名的NP=P？的猜想。

解決這個猜想，無非兩種可能，一種是找到一個這樣的算法，只要針對某個特定NP完全問題找到一個算法，所有這類問題都可以迎刃而解了，因為他們可以轉化為同一個問題。另外的一種可能，就是這樣的算法是不存在的。那么就要從數學理論上證明它為什麼不存在。

搜尋方法

近鄰法

近鄰法（nearest neighbor)　推銷員從某個城鎮出發，永遠選擇前往最近且尚未去過的城鎮，最後再返回原先的出發點。這方法簡單，也許是多數人的直覺做法，但是近鄰法的短視使其表現非常不好，通常後段的路程會非常痛苦。

插入法

插入法（insertion)　先產生連線部分點的子路線，再根據某種法則將其它的點逐一加入路線。比如最近插入法（nearest insertion），先針對外圍的點建構子路線，然後從剩餘的點裡面評估何者加入後路線總長度增加的幅度最小，再將這個點加入路線。又比如最遠插入法（farthest insertion），是從剩餘的點裡面選擇距離子路線最遠的點，有點先苦後甜的滋味。

模擬退火算法

模擬退火算法（Simulated Annealing) 來源於固體退火原理，將固體加溫至充分高，再讓其徐徐冷卻，加溫時，固體內部粒子隨溫升變為無序狀，內能增大，而徐徐冷卻時粒子漸趨有序，在每個溫度都達到平衡態，最後在常溫時達到基態，內能減為最小。根據Metropolis準則，粒子在溫度T時趨於平衡的機率為e-ΔE/(kT），其中E為溫度T時的內能，ΔE為其改變數，k為Boltzmann常數。用固體退火模擬組合最佳化問題，將內能E模擬為目標函式值f，溫度T演化成控制參數t，即得到解組合最佳化問題的模擬退火算法：由初始解i和控制參數初值t開始，對當前解重複“產生新解→計算目標函式差→接受或捨棄”的疊代，並逐步衰減t值，算法終止時的當前解即為所得近似最優解。

遺傳算法

遺傳算法是仿真生物遺傳學和自然選擇機理，通過人工方式所構造的一類搜尋算法，從某種程度上說遺傳算法是對生物進化過程進行的數學方式仿真。生物種群的生存過程普遍遵循達爾文進化準則，群體中的個體根據對環境的適應能力而被大自然所選擇或淘汰。進化過程的結果反映在個體的結構上，其染色體包含若干基因，相應的表現型和基因型的聯繫體現了個體的外部特性與內部機理間邏輯關係。通過個體之間的交叉、變異來適應大自然環境。生物染色體用數學方式或計算機方式來體現就是一串數碼，仍叫染色體，有時也叫個體；適應能力是對應著一個染色體的一個數值來衡量；染色體的選擇或淘汰則按所面對的問題是求最大還是最小來進行。

神經網路算法

根據一個簡化的統計，人腦由百億條神經組成 — 每條神經平均連結到其它幾千條神經。通過這種連結方式，神經可以收發不同數量的能量。神經的一個非常重要的功能是它們對能量的接受並不是立即作出回響，而是將它們累加起來，當這個累加的總和達到某個臨界閾值時，它們將它們自己的那部分能量傳送給其它的神經。大腦通過調節這些連結的數目和強度進行學習。儘管這是個生物行為的簡化描述。但同樣可以充分有力地被看作是神經網路的模型。

填字遊戲

填字遊戲是一種最常見的益智紙上遊戲，也是NP完全問題之一，遊戲一般給出一個矩形的表格。這個表格被分割為若干個大小相同的方格，方格的顏色有白色與黑色兩種。白色的方格組成一些交叉的行與列，行列的長度不等。玩家根據題目所提供的有關信息，將答案填入這些行與列之中，每個白色方格中只能填入一個字。一般地說，題目給出的每一條信息就是對應的一行或一列的解題線索。在行與列交叉的地方，玩家必須保證在交叉的方格中填入的字同時滿足題目中對行與列的要求。（詳見填字遊戲）

NP完全問題之填數遊戲

相關

最常被引用的結果之一設計神喻。假想你有一個魔法機器可以解決單個問題，例如決定一個給定的數字是否為質數，但可以瞬間解決這個問題。我們的新問題是，若我們被允許任意利用這個機器，是否存在我們可以在多項式時間內驗證但無法在多項式時間內解決的問題？結果是，依賴於機器能解決的問題，P = NP和P ≠ NP二者都可以證明。這個結論的後果是，任何可以修改來證明該機器的存在性的結果不能解決問題。不幸的是，幾乎所有經典的方法和大部分已知的方法可以這樣修改（我們稱它們在相對化）。

如果這還不算太糟的話，1993年Razborov和Rudich證明的一個結果表明，給定一個特定的可信的假設，在某種意義下“自然”的證明不能解決P = NP問題。這表明一些現在似乎最有希望的方法不太可能成功。隨著更多這類的定理得到證明，該定理的可能證明有越來越多的陷阱要規避。這實際上也是為什麼NP完全問題有用的原因：若有一個多項式時間算法，或者沒有一個這樣的算法，對於NP完全問題存在，這將用一種相信不被上述結果排除在外的方法來解決P = NP問題。P=NP問題可以用邏輯命題的特定類的可表達性的術語來重新表述。所有P中的語言可以用一階邏輯加上最小不動點操作（實際上，這允許了遞歸函式的定義）來表達。類似地，NP是可以用存在性二階邏輯來表達—也就是，在關係、函式、和子集上排除了全域量詞的二階邏輯。多項式等級，PH中的語言對應與所有的二階邏輯。這樣，“P是NP的真子集嗎”這樣的問題可以表述為“是否存在性二階邏輯能夠表達帶最小不動點操作的一階邏輯的所不能表達的語言？”

普林斯頓大學計算機系樓將二進制代碼表述的“P=NP?”問題刻進頂樓西面的磚頭上。如果證明了P=NP，磚頭可以很方便的換成表示“P=NP！”。康奈爾大學的Hubert Chen博士提供了這個玩笑式的P不等於NP的證明：“反證法。設P = NP。令y為一個P = NP的證明。證明y可以用一個合格的計算機科學家在多項式時間內驗證，我們認定這樣的科學家的存在性為真。但是，因為P = NP，該證明y可以在多項式時間內由這樣的科學家發現。但是這樣的發現還沒有發生（雖然這樣的科學家試圖發現這樣的一個證明），我們得到矛盾。

最新情況

2010年8月6日，HP LAB的 Vinay Deolalikar 教授宣布證明了P!=NP，證明文章已經傳送到該問題各相關領域專家手中，等待檢驗，在他的主頁上，證明過程已經公布（PDF格式共103頁），但在8月15日，人們關於論文的看法——即證明不能成立——已經趨於穩定（當然這不能排除大家都同時犯了錯誤的可能性），隨後的發言越來越多地集中於更抽象的層面，並且至今仍在繼續。

NP完全問題說明

論NP=P？

NP=P，概括的說就是3句話：

1.任意簡單無向圖的最大團問題等於其對應的“任意兩個頂點的距離不大於2的圖”——可以稱之為理想圖的最大團問題；

2.任意理想圖的圖著色問題是多項式時間問題；

3.任意理想圖，其圖著色問題可在多項式時間內轉換為它的最大團問題。

證明大綱：

定理1.設G=（V,E）是簡單無向圖，va、vb是G中距離大於2的兩個頂點，E'=E∪{（va，vb）}，則G'=(V，E')與G有相同的最大團。
證明：顯然。
推論：對任意簡單無向圖G=（V,E），存在簡單無向圖G'=(V，E')，滿足：
（1）E⊆E'；
（2）G'中任意兩個頂點的距離不大於2；
（3）G'與G有相同的最大團。

定理2.設G=（V,E）是n階簡單無向圖，n≥3，G中任意兩個頂點的距離不大於2，則存在n的多項式時間算法，可在該算法下，解決G的圖著色問題，即確定G的頂點色數。
證明思路與算法：易知G是k-部圖（不一定、也無須是完全k-部圖）。
算法：設v是G中度最大的頂點，顯然v的鄰點應該與v著色不同。在距離v為2的
頂點中，依次選取G中度最大且互不相鄰的頂點，得到包含v的一個極大獨立集V1，
設V=V1∪V2,V1∩V2=Ø，G去掉V1中所有頂點（及其關聯邊）得到圖
G2=(V2，E2)。則可以證明G2的頂點色數比G的頂點色數小1；且G2去掉度
小於2的頂點（若這樣的頂點存在）後，任意兩個頂點的距離也是不大於2的。
由遞歸關係可知G的頂點色數可以在n的多項式時間內確定。

定理3.設G=（V,E）是n階簡單無向圖，n≥3，G中任意兩個頂點的距離不大於2，則G的圖著色問題（頂點色數問題）可以在n的多項式時間內轉換為G的最大團問題。

前景

當今時代，在純粹科學研究，通信、交通運輸、工業設計和企事業管理部門，在社會軍事、政治和商業的鬥爭中湧現出大量的NP問題。若按經典的純粹數學家們所熟悉的窮舉方法求解，則計算時間動輒達到天文數字，根本沒有實用價值。數學界許多有經驗的人認為對於這些問題根本上就不存在完整、精確、而又不是太慢的求解算法。NP=P？可能是這個世紀最重要的數學問題了。