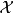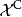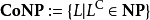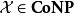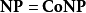在計算複雜度理論上,反NP類是複雜度類的其中一類。反NP複雜度,是高效率而又可核實地證明命題為錯的組群,當中的佼佼者是立即找到反例存在。
基本介紹
- 中文名:反NP
- 外文名:Anti-NP
- 領域:理論信息學
定義,與其他複雜度的關係,套用,
定義
其中一個NP完全問題的例子是子集合加總問題:給一個整數集合,問是否存在某個非空子集中的數字和為0? 例:給定集合{−7, −3, −2, 5, 8},答案是是,因為子集合{−3, −2, 5}的數字和是0。
補全問題在反NP中就會要求:給有限的整數集,是否每個非空子集有一個非零總和?你的證明只要必須給出事例,敘述"沒有"指定求和到零的一個非空子集,而這證明必須可以在合理時間內驗證。
與其他複雜度的關係
複雜度P,是多項式時間可解的問題集合,是一個NP和反NP的子集。P通常認定是一個在此兩類別下的嚴格子集(但無法驗證是落在兩個集合的哪一邊)。NP和反NP通常認為是不相等的。如果那樣,NP完全問題將不會落在反NP問題中,且反NP完全問題將不會落在NP中。
本問題可由下述步驟粗略證明:假設有個NP完全問題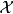 處於反NP問題的集合中,由於所有NP問題可被變換成
處於反NP問題的集合中,由於所有NP問題可被變換成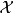 問題,因此我們可以為所有NP問題建造一個可在多項式時間判定其補性質的非確定型圖靈機,意即NP是反NP的子集。因此NP問題的補集合是一個反NP問題的補集合,意即反NP是NP的子集。由於我們已知NP是反NP的子集,因此表示這兩個集合是一樣的,這證明了沒有反NP完全問題可在NP類之中的性質是對稱的(Symmetrical)。
問題,因此我們可以為所有NP問題建造一個可在多項式時間判定其補性質的非確定型圖靈機,意即NP是反NP的子集。因此NP問題的補集合是一個反NP問題的補集合,意即反NP是NP的子集。由於我們已知NP是反NP的子集,因此表示這兩個集合是一樣的,這證明了沒有反NP完全問題可在NP類之中的性質是對稱的(Symmetrical)。
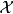
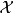
若: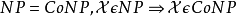
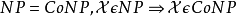
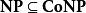
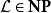
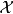
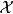
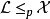
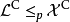
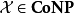
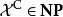
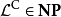
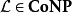
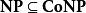
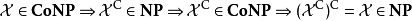
如果一個問題可被證同時為NP與反NP,則通常我們將會視作本問題不是NP完全命題的強力假設(若非如此,則NP相等於反NP)。
套用
一個同時在NP與反NP集合的有名問題是整數分解:給兩個正整數m與n,決定m是否有小於n且大於1的因數。
第一個問題的方法很清晰:如果m的確存在一個滿足條件的因子,則長除法即可驗證;另一個問題的方法就困難且精妙多了:你必須將m的所有質數因子列出,並為每個因子提供質數性質的證明。
整數因子分解常與質數性質問題混淆在一起,整數因子化據信是NP或反NP,而質數問題落在類別P。