NP問題是指存在多項式算法能夠驗證的非決定性問題,而其中NP完全問題又是最有可能不是P問題的問題類型。所有的NP問題都可以用多項式時間歸約到他們中的一個。所以顯然NP完全的問題具有如下性質:它可以在多項式時間內求解,若且唯若所有的其他的NP-完全問題也可以在多項式時間內求解。
基本介紹
- 中文名:NP問題
- 外文名:Non-Deterministic Polynomial Problems
- 縮寫:NP
- 特點:它可以在多項式時間內驗證
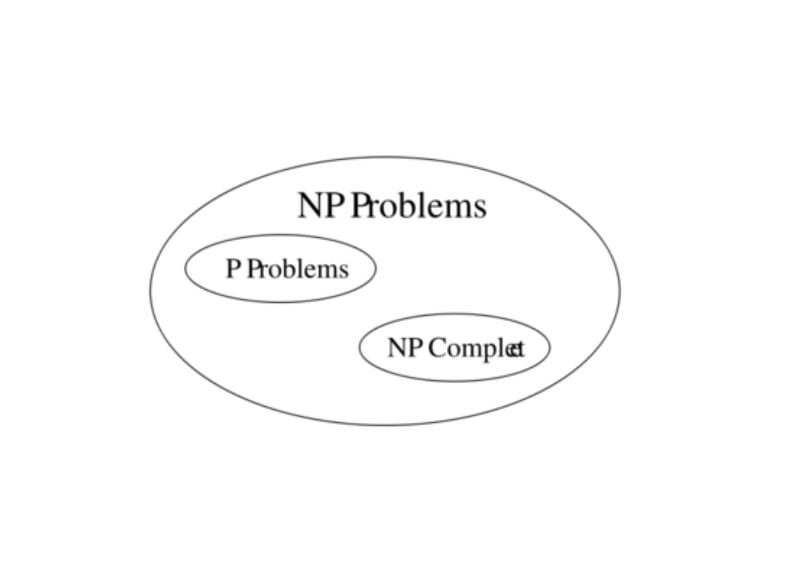
NP問題是指存在多項式算法能夠驗證的非決定性問題,而其中NP完全問題又是最有可能不是P問題的問題類型。所有的NP問題都可以用多項式時間歸約到他們中的一個。所以顯然NP完全的問題具有如下性質:它可以在多項式時間內求解,若且唯若所有的其他的NP-完全問題也可以在多項式時間內求解。
NP完全問題(NP-C問題),是世界七大數學難題之一。 NP的英文全稱是Non-deterministic Polynomial的問題,即多項式複雜程度的非確定性問題。簡單的寫法是 NP=P?,問題...
NP問題是指存在多項式算法能夠驗證的非決定性問題,而其中NP完全問題又是最有可能不是P問題的問題類型。所有的NP問題都可以用多項式時間歸約到他們中的一個。所以...
P對NP問題是克雷數學研究所高額懸賞的七個千禧年難題之一,同時也是計算機科學領域的最大難題,關係到計算機完成一項任務的速度到底有多快。...
NP的英文全稱是Non-deterministic Polynomial的問題,即多項式複雜程度的非確定性問題。...
NP-hard,指所有NP問題都能在多項式時間複雜度內歸約到的問題...... NP-hard,指所有NP問題都能在多項式時間複雜度內歸約到的問題 外文名 NP-hard 全稱 non-...
P-NP I}}題(P-NP problem)亦稱P=? NP問題,計算複雜性理論以及計算機理論中最重要的一個未解決問題。它問在多項式時間界下,確定型圖機接受的語言類是與非...
npc,指NP完全問題(Non-deterministic Polynomial complete problem)。簡單的說,如果任何一個NP問題都能通過一個多項式時間算法轉換為某個NP問題,那么這個NP問題就稱為...
NP完全或NP完備(NP-Complete,縮寫為 NP-C 或 NPC),是計算複雜度理論中,決定性問題的等級之一。NPC 問題,是NP(非決定性多項式時間)中最難的決定性問題。因此...
簡介NP,即非確定性多項式 Non-deterministic polynomial的縮寫。所謂非確定性,就是指可以用一定數量的運算去解決多項式時間內可解決的問題。NP 問題通俗來說是其解的...
《NP難解問題的近似算法》是1998年世界圖書出版公司出版的圖書,作者是Dorit S.Hochbaum。...
計算複雜性理論中的一個重要概念,它表征某些問題的固有複雜度。一旦確定一類問題具有NP完全性時,就可知道這類問題實際上是具有相當複雜程度的困難問題。...
非定常多項式(英語:non-deterministic polynomial,縮寫:NP)時間複雜性類,或稱非確定性多項式時間複雜性類,包含了可以在多項式時間內,對一個判定性算法問題的實例,一...
旅行商問題,即TSP問題(Traveling Salesman Problem)又譯為旅行推銷員問題、貨郎擔問題,是數學領域中著名問題之一。假設有一個旅行商人要拜訪n個城市,他必須選擇所要...
在計算複雜度理論上,反NP類是複雜度類的其中一類。反NP複雜度,是高效率而又可核實地證明命題為錯的組群,當中的佼佼者是立即找到反例存在。...
NPC問題是在P問題與NP問題上的一個重大進展在20世紀70年代初由Cook S和Levin L完成,他們發現NP中的某些問題的複雜性與整個類的複雜性相關聯.這些問題中任何一個...
np小說一般指的是一個女/男主角和n個男/女主角發生的故事,理所當然,小說的結局也是一女/男和n女/男的結局收場的。還有其他情況就是n個男xn男、n女xn女、n...
P/NP問題是在理論信息學中計算複雜度理論領域裡至今沒有解決的問題,它被“克雷數學研究所”(Clay Mathematics Institute, 簡稱CMI)在千禧年大獎難題中收錄。 P/NP...
P/NP問題是在理論信息學中計算複雜度理論領域裡至今未被解決的問題,也是克雷數學研究所七個千禧年大獎難題之一。P/NP問題中包含了複雜度類P與NP的關係。1971年...
在計算複雜度理論中,分團問題(clique problem)是圖論中的一個NP完全(NP-complete)問題。...
近世計算理論導引——NP難度問題的背景、前景及其求解算法研究 數學機械化叢書 -5黃文奇,許如初 著科學出版社2004年6月出版定價:20.00語種:中文標準書號:7-03-...
《評《來吧,自由的翻滾!》NP人選的處理問題》是叨叨的刀刀創作的網路小說,發表於晉江文學網。...
旅行推銷員問題(英語:Travelling salesman problem, TSP)是這樣一個問題:給定一系列城市和每對城市之間的距離,求解訪問每一座城市一次並回到起始城市的最短迴路。它...
這七個“世界難題”是:NP完全問題、霍奇猜想、龐加萊猜想、黎曼假設、楊-米爾斯存在性和質量缺口、納衛爾-斯托可方程、BSD猜想。這七個問題都被懸賞一百萬美元。....
