基本介紹
- 中文名:收斂級數
- 外文名:Convergent series
- 提出者:柯西
- 提出時間:1821年
- 分類:收斂級數和絕對收斂級數
- 必要條件:通項的極限為0
預備知識

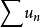
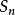
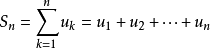
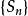
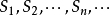

定義

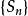

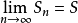




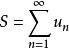
基本性質
性質1


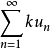
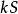

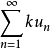
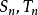
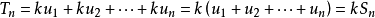

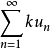
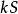
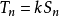
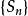
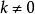
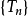
性質2

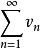
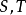
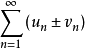
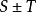

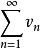
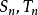
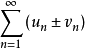
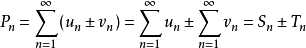
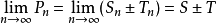
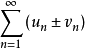
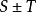
性質3
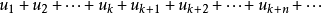
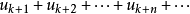
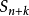
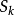
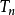
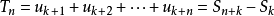
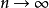
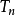
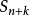
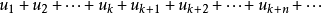
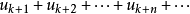
性質4

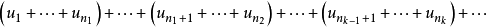

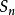
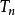
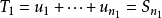
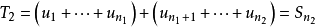
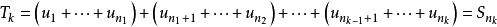
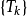
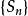
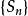
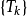
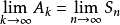
性質5
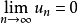
級數收斂性
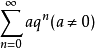
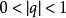
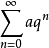

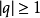
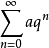
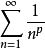
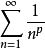
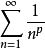


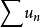
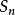
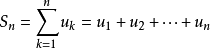
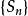
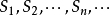


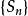

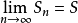




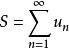


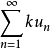
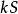

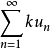
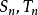
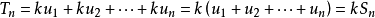

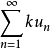
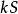
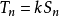
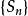
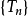

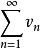
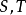
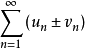
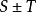

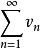
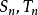
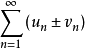
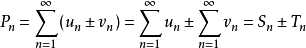
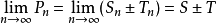
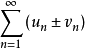
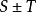
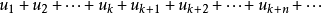
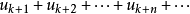
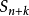
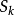
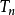
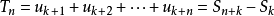
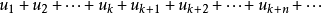
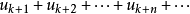

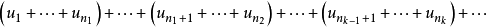

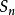
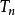
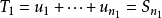
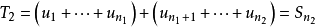
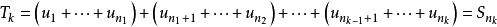
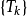
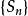
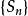
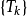
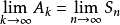
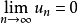
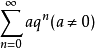
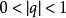
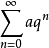

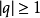
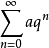
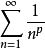
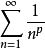
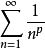
收斂級數(convergent series)是柯西於1821年引進的,它是指部分和序列的極限存在的級數。收斂級數分條件收斂級數和絕對收斂級數兩大類,其性質與有限和(有限項相加)...
級數是指將數列的項依次用加號連線起來的函式。典型的級數有正項級數、交錯級數、冪級數、傅立葉級數等。級數理論是分析學的一個分支;它與另一個分支微積分學一...
無窮級數是研究有次序的可數或者無窮個數函式的和的收斂性及和的數值的方法,理論以數項級數為基礎,數項級數有發散性和收斂性的區別。只有無窮級數收斂時有一個和...
無條件收斂級數(unconditionally convergentseries)主要包括數值級數的無條件收斂和Banach空間內級數的無條件收斂,兩者的定義是相同的,是指任何重排均收斂的級數。換句...
條件收斂級數是指收斂但不絕對收斂的級數,級數本身收斂但不絕對收斂。...... 條件收斂級數是指收斂但不絕對收斂的級數,級數本身收斂但不絕對收斂。中文名 條件收斂...
數項級數的收斂性問題是數學分析中研究的基本內容之一。數項級數主要分為正項級數和一般項級數,一般項級數的收斂性判別問題要比正項級數複雜。在此,我們只討論...
發散級數指不收斂的級數。一個數項級數如果不收斂,就稱為發散,此級數稱為發散級數。一個函式項級數如果在(各項的定義域內)某點不收斂,就稱在此點發散,此點稱...
收斂是一個經濟學、數學名詞,是研究函式的一個重要工具,是指會聚於一點,向某一值靠近。收斂類型有收斂數列、函式收斂、全局收斂、局部收斂。...
條件收斂是一種微積分上的概念。如果級數ΣUn收斂,而Σ∣Un∣發散,則稱級數ΣUn條件收斂。...
正項級數,是一種數學用語。在級數理論中,正項級數是非常重要的一種,對一般級數的研究有時可以通過對正項級數的研究來獲得結果,就像非負函式廣義積分和一般廣義...
數學分析的基本概念之一,它與“有確定的(或有限的)極限”同義,“收斂於……”相當於說“極限是……(確定的點或有限的數)”。在一些一般性敘述中,收斂和收斂...
在數學中,泰勒級數(英語:Taylor series)用無限項連加式——級數來表示一個函式,這些相加的項由函式在某一點的導數求得。泰勒級數是以於1715年發表了泰勒公式的...
重級數(multiple series)也稱多重級數,k重級數等,是重序列的形式和,多重級數的理論和性質等可效仿二重級數的理論和性質加以推廣得到。...
疊級數(repeated series)亦稱累級數,指各項均為級數的級數,即表達式∑∞m=1∑∞n=1amn,其中{amn}為二重序列。對疊級數,可以用普通級數的有關概念來定義其收斂...
冪級數,是數學分析當中重要概念之一,是指在級數的每一項均為與級數項序號n相對應的以常數倍的(x-a)的n次方(n是從0開始計數的整數,a為常數)。冪級數是數學...
在數學中,傅立葉級數是一種三角級數,傅立葉級數也常稱為三角級數。但並不是所有三角級數都是傅立葉級數。一個有趣的問題是給定一個三角級數,當x取什麼值時...
《數乘收斂級數與無窮矩陣理論》是曲文波的論文。...... 《數乘收斂級數與無窮矩陣理論》是曲文波的論文。中文名 數乘收斂級數與無窮矩陣理論 外文名 Multiplier...
對於無窮級數∑an,其部分和為Sn=∑ak:。如果部分和的數列〔S1,S2,S3,...〕...... .如果級數∑an收斂,但級數∑∣an∣發散,則稱此級數是條件收斂的。假設...
一致收斂性是函式列或函式項級數的一種性質。一致收斂函式的判別方法有很多種,最常見的有Cauchy判別法、Abel判別法、Dirichlete判別法等。一致收斂函式具有連續性、...
已知其在一個給定的點集C上收斂得足夠快的某些多項式序列,必在一個把C包含在內的點集上收斂,這個現象就稱為過收斂。...
