基本介紹
- 中文名:擴張映射
- 外文名:expanding map
- 適用範圍:數理科學
定義


擴張映射原理
定理





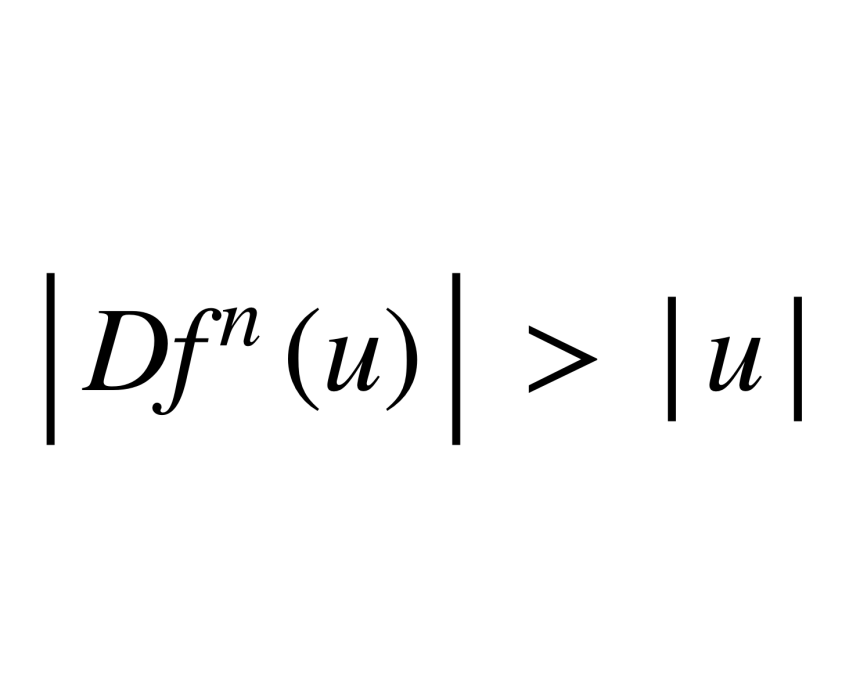







擴張映射是撒布(Shub, M.)在1969年最先研究得到的一類結構穩定的半動力系統。擴張映射是結構穩定的,並且具有有理的夸函式。因此,擴張映射是對微分同胚理論研究的...
度量空間亦稱距離空間。一種拓撲空間,其上的拓撲由距離決定。可擴映射(expansive map)是一類重要的動力系統。設(M,d)是一個度量空間,f:M→M是一連續映射,如果...
擴張定理(extension theorem)是反映正規空間中連續映射的擴張性質的一條定理,是超實數域到超結構的擴張定理...
映射的限制(restriction of a mapping)又稱映射的收縮、部分映射,是一種特殊的映射,是與對應的限制、關係的限制同義的概念。...
安諾索夫可微映射(Anosov differentiablemap)是比安諾索夫微分同胚和擴張映射更廣的一類。...
初等擴張原理斷言:V(R)的初等部分中的句子,即R的一階謂詞中的句子在R中為真,若且唯若*φ在*R中為真。...
與集值映射有關的一個概念.設X,Y為拓撲空間,AX,F:A→Y為集值連續映射,若集值映射G:X→Y滿足:1.對於任意二EA,F(二)=CU(二);2.G為連續映射;則稱G...
單純映射(simplicial map)是聯繫復形的多面體之間的一類重要映射。它是從復形K的多面體|K|到復形L的多面體|L|的連續映射,任何連續映射在某種意義下可用它逼近,可...
擴張不變集(expanding invariant set)離散微分半動力系統中較之擴張映射更廣泛的研究對象,是一個重要的不變集.設M是黎曼流形,UCM是具有緊緻閉包的開集,八CU是....
f是全連續映射,若且唯若f是0集壓縮的。常取非緊性測度為集-非緊性測度或球-非緊性測度。這時,巴拿赫k壓縮映射是k集壓縮的,非擴張映射是1-集壓縮的,但嚴格...
全實擴張(totally real extension)一類特殊的實擴張域.設K是實域F'的一個擴張,若F'上的每個序都可拓展為K上的一個序,則稱K是F的一個全實擴張.換言之,若...
標準部分映射(standard part map)是有限超實數集到實數集的一個映射。設Fin(*R)是一切有限超實數集,則映射st:Fin(*R)→R,st(y)=x,若且唯若x≈y,稱為...
蒂茨擴張定理(Tietze extension theorem)反映正規空間中連續映射的擴張性質的一條定理,在拓撲學中有重要套用。...
模擴張(modular extension)是比可分擴張更廣泛的一類域擴張。特徵為p≠0的域擴張K/F,若對於每個整數n≥1,K與F都是線性分離的,則稱為模擴張。可分擴張就是模...
雙曲線性映射亦稱雙曲線性同構,是沿一個方向擴張,沿另一個方向收縮的可逆線性映射。線性映射的雙曲性經過小擾動之後不至於被破壞,這一性質在動力系統結構穩定性的...
阿廷映射(Artin mapping)是理想群(或伊代爾群)到伽羅瓦群的映射。它是類域論的基石之一。伊代爾群是一種特殊的群。即各分量為諸局部域元素的某些向量(其分量...
《映射疊代與混沌動力系統》是2013年1月科學出版社出版的圖書,作者是廖公夫、王立冬、范欽傑。...
零倫映射(null-homotopic map)是一類特殊的映射,設X,Y都是拓撲空間,若映射f:X→Y同倫於某常值映射f0:X→Y,則它稱為零倫的。從映射同倫觀點看,最簡單的...
可許亨澤爾擴張(allowable Henselian exten-sion)是一類重要的亨澤爾擴張。藉助這類擴張,欲求賦值環在某個有限擴張上的拓展個數,只須考察此有限擴張到代數閉擴張中...
瓦勒曼緊化(Wallman compactification)一種特殊的緊化.對於每個T,空間X,可構造一個以X為稠密子空間的緊T:空間wX,使得對於任意緊T:空間Z與任意連續映射f : X-...
