基本介紹
- 中文名:擴充實值函式
- 外文名:extended real-valued function
- 適用範圍:數理科學
簡介
推論
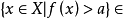
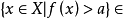
擴充實值函式是取擴充實數值的函式,即可取無窮值的函式。實變函式論中的可測函式一般屬於擴充實值函式。...
若實值集函式的值可允許取+∞或-∞,則稱此集函式為擴充實值集函式。...... 若實值集函式的值可允許取+∞或-∞,則稱此集函式為擴充實值集函式。...
廣義原函式是原函式概念的推廣。若f(x)及F(x)是區間[a,b]上的擴充實值函式,導數F'(x)幾乎處處存在並等於f(x),則F(x)稱為f(x)的廣義原函式。...
下極限函式是為判斷函式下半連續性而引進的一個概念。設f(x)是定義在點集E上的擴充實值函式,若在閉包E內的點x的δ鄰域與E的交內,函式f所取的值的下確界...
波萊爾可測函式(Borel measurable function)亦稱波萊爾函式,是與波萊爾集相適應的可測函式。設f(x)是定義在波萊爾集B⊂Rn上的擴充實值函式,若對任意實數α,點集...
重要的(數值)集函式有測度、集上的積分等。若實值集函式的值可允許取+∞或-∞,則稱此集函式為擴充實值集函式。集函式性質 編輯 關於集函式,也可引入單調性...
勒貝格可測函式簡稱(L)可測函式,是比連續函式更廣的一類函式。定義在(L)零測度集上的任何實值函式以及區間上的半連續函式都是(L)可測函式。定義在(L)可測集...
共軛函式亦稱對偶函式、極化函式,函式的某種對偶變換。設f為實線性空間X上的擴充實值函式,X*為X的某個對偶空間,即由X上的一些線性函式所構成的實空間,那么f的...
設g(x)是定義在R上的一個單調上升的右連續函式,集E是關於g(x)的(L-S)可測集,f(x)是定義在E上的一個擴充實值函式。若對任意實數α,集{x∈E|f(x)...
嚴格擬凸函式(strictly quasi-convex function)是凸集上的一類函式。設S是線性空間中的非空凸集,f是S上的實值函式。若對任何實數α∈(0,1)和任意的x1,x2∈S...
若f是可測空間(Ω,F)上的擴充實值函式,則f在(Ω,F)上可測的充分必要條件是f為(Ω,F)到(R,B)中的可測映射,其中R為擴充實數空間,B為廣義波萊爾集類。...
在傅立葉分析的數學領域,共軛傅立葉級數是通過正式實現傅立葉級數作為單位圓盤上全息函式的實部的邊界值產生的。 由該函式的虛部定義了共軛序列。 齊格蒙德(Zygmund...
共軛函式亦稱對偶函式、極化函式,函式的某種對偶變換。設f為實線性空間X上的擴充實值函式,X*為X的某個對偶空間,即由X上的一些線性函式所構成的實空間,那么f的...
水平集(level set)的基本思想是將界面看成高一維空間中某一函式ψ(稱為水平集函式)的零水平集,同時界面的演化也擴充到高一維的空間中。我們將水平集函式按照它...
