擬循環p群,數學術語。
基本介紹
- 中文名:擬循環p群
- 外文名:quasicyclic p-group
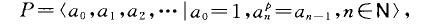

擬循環p群,數學術語。
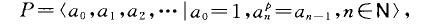
生物圈2號(Biosphere 2)是美國建於亞利桑那州圖森市以北沙漠中的一座微型人工生態循環系統,為了與生物圈1號(地球本身)區分而得此名,它由美國前橄欖球運動員約翰·艾倫發起,是愛德華·P·巴斯及其他人員主持建造的人造封閉生態系統。並與幾家財團聯手出資,主要投資者為美國石油大王洛克菲勒委託空間生物圈風險投資...
循環硬化,力學術語。在低周疲勞的循環載入初期,材料對循環載入的回響是一個由不穩定向穩定過渡的過程。此過程可分別用應力控制下的應變-時間曲線和應變控制下的應力-時間曲線描述。循環硬化是材料在循環過程中變形抗力不斷提高、應變逐漸減小的現象。循環軟化則是材料在循環過程中變形抗力不斷減小而應變逐漸增加的現象...
我們得到了Γ的一個具體描述,當G是基本p群和循環p群時,給出了K_2(ZG/nΓ)階數的下界,並證明了它是平凡群若且唯若n是沒有平方因子的整數。當p是正則素數時,對於有限交換p-群給出了K_2(ZG)階數的下界。確定了K_2(C_2×C_2)的結構,同時證明了Wh_2(C_2×C_2) 是秩為2的初等2群。這是非...
我們利用由環的Cartesian塊誘導的Mayer-Vietoris序列得到了當G為有限交換p-群時K2(ZG)的階數的一個下界,並且給出了當p為奇素數時K2(ZG)的p-秩的下界,其中G是循環p-群或基本交換p-群。同時我們還給出了對較小的素數p,當G是循環p-群或基本交換p-群時K2(ZG)的結構。當F是特徵為p的有限域,對於G的階數...
是一個阿貝爾群(運算表為加法), 是一個正整數,考慮 的如下子集 易見它是 的一個子群. 若 , 即對 中的任一元素 ,均存在 使得 ,則稱 是 -可除的. 若對任意正整數 , 都是 -可除的,則稱 是可除的. 阿貝爾群G是可除群,若且唯若它同構於一些有理數加群Q和擬循環群的直和;而且,...
性質1:二面體群是非可換p群。我們知道,群 與關於四個文字對稱群 的子群同構,後者是非可換群,故性質1成立。性質2:二面體群與其自同構群同構。我們可以直接驗證,二面體群可以由兩個生成元分別記做f=(1234)和r=(24),且滿足關係:生成的,式中1表示四個文字的恆等置換。綜合以上所述。二面體群共有十...
完全刻畫包含正則p-群的擬本原和二部擬本原群,並分類p-群上的擬本原和二部擬本原的局部本原Cayley圖;刻畫階為兩個素數冪乘積的群上的局部本原Cayley圖。(4)分類包含亞循環傳遞子群的擬本原群,並套用分類的結果完成亞循環群的點本原的局部本原Cayley圖的分類。科研成果 ...
群G是可除阿貝爾群,若且唯若對任意素數p,G的每一元素都有無限的p高度。阿貝爾群G是可除群,若且唯若它同構於一些有理數加群Q和擬循環群的直和;而且,每一阿貝爾群同構於可除阿貝爾群的一個子群。阿貝爾群G的任意可除子群D恆為G的直和項。一個阿貝爾群,若它不含非平凡的可除子群,則稱此群為既約...
單位定理(unit theorem)域的單位群的結構定理.若F,為整體域(即有理數域Q或有限域上有理函式域F,, ct>的有限擴張),s為包含其所有無限素除子的有限集合,則F的s單位群U。是、一1個無限循環群與有限循環群W的直積,即Us-Z`-' XW,式中、為s的元素個數,W為F中的單位根形成的群.特別地,若F'為...
群代數半單性定理(semisimplicity theorem ofgroup algebra)指的是群代數的雅各布森半單性判別定理。設G是群,K是域且K不是它的素域上代數,若chK=0或chK=p>0時,G不含p階元,則K[G]是雅各布森半單(簡稱J半單)。雅各布森半單亦稱J半單。一類重要的環。若環R的雅各布森根J(R)=0,則R稱為半本原環...
(1)初始化:設定進化代數計數器t=0,設定最大進化代數T,隨機生成M個個體作為初始群體P(0)。(2)個體評價:計算群體P(t)中各個個體的適應度。(3)選擇運算:將選擇運算元作用於群體。選擇的目的是把最佳化的個體直接遺傳到下一代或通過配對交叉產生新的個體再遺傳到下一代。選擇操作是建立在群體中個體的適應度...
我們用△(i)記P(i)的使得其合成因子具有形式E(j)(j≤i)的極大商模。對偶地,用(i)記Q(i)的使得其合成因子具有形式E(j)(j≤i)的極大子模,用△與記由△(i)與(i),i∈Λ,構成的模類。代數A(更確切地說,二元對(A,Λ))被叫做擬遺傳代數,如果 (i)End(△(i))k,...
$$z\mapsto Tr(P(D^2+1)^{-z/2})$$ \noindent 具有一個到$\mathbb$上的僅有單重極點的亞純延拓.這樣$res(P)$就是這個函式在0點的留數.重要的是,Wodzicki留數由我們的譜三元組完全確定,而且這個留數是一個跡: 對於任意兩個擬微分運算元,我們有 $res PQ=resQP$.同時,這還是$V$上的擬微分運算元...
有限群的研究起源很早,其形成時期是與柯西、拉格朗日、高斯、阿貝爾以及後來的伽羅瓦、若爾當等人的名字相聯繫的。如何確定可解群和單群是抽象群理論建立後的一個重要發展方向。德國數學家赫爾德在1889年以後的若干年內,詳細地研究了單群和可解群,證明:一個素數階循環群是單群,n個(n≥5)文字的全部偶置換組成的...
(3)植物物種多樣性促進了尾礦土壤營養元素(C、N、P)的循環和累積(P<0.05)。其主要作用機制很可能是植物多樣性不僅提高了土壤微生物的多樣性而且提高一些與土壤C、N、P循環相關的細菌和真菌的相對豐度。這些研究結果揭示物種多樣性影響重金屬尾礦生態恢復效率的內在機理,為物種多樣性在重金屬尾礦生態恢復中的...
相點陣圖表示兩個種群的密度將按封閉環的軌道逆時針方向無限循環,其中心點即為平衡點(N=r2/θ=0.5/0.02=25,P=r1/ε=1.0/0.1=10),通過平衡點作互相垂直的線,將相點陣圖分為4塊,在垂直線右面捕食者種群增加,在左面減少,在水平線下面,獵物種群增加,在上面減少。因此,洛特卡-沃爾泰拉模型表明獵物-捕食...
同時,隨著“A品牌”在市場知名度的提升,終端消費者對產品的需求也拉動了小超市和經銷商對A品牌產品的興趣,使終端開發進入一個良性循環之中,有助於其它零售終端和分銷渠道的建設。在北京以外的全國市場,出於資源優勢互補的考慮,我們確立了以分銷為主的渠道模式。在分銷上,綜合考慮了企業所面臨的市場因素、產品...
血液動力學是生物力學的一個分支,其主要任務是套用流體力學的理論和方法研究血液沿血管循環流動的原因、條件、狀態以及各種影響因素,以闡明血液流動的規律、生理意義及與疾病的關係。血液循環系統由心臟、血液和血管構成。與一般的流體動力系統相比,血液循環系統具有許多特點。首先,血管是有無數分支的彈性管,血管在維持...
葉綠體(英語:chloroplast)是綠色植物和藻類等真核自養生物細胞中專業化亞單元的細胞器。其主要作用是進行光合作用,其中含有的光合色素葉綠素從太陽光捕獲能量,並將其存儲在能量儲存分子ATP和NADPH,同時從水中釋放氧氣。然後,它們使用ATP和NADPH,在被稱為卡爾文循環的過程中從二氧化碳製造有機分子。葉綠體實施許多其它...
如果用登山來比喻,演化就像是走盤山路,螺旋上升,不斷縮短與山頂的距離;而內卷則是在山腳下或半山腰不斷循環,永遠無法登頂。現指同行間競相付出更多努力以爭奪有限資源,從而導致個體“收益努力比”下降的現象。可以看作是努力的“通貨膨脹”。流行背景 2020年下半年,有幾張圖片刷屏:有人騎在腳踏車上看書,有...
從而回答了法國著名組合數論專家Hamidoune2003年提出的一個公開問題。(4)給出了有限群(不必交換)的Davenport常數的一個好的上界. 設G是一個n階有限群, p為n的最小素因子,我們證明了D(G)=n/p+p-1.(5)首次提出研究Erdos-Ginzburg-Ziv定理在交換半群上的推廣和精確化問題,提出了Gao定理E(G)=D(G)...
休森同時展示了一家新的 高超音速飛行器 概念圖,類似HAWC但是更接近於“基於渦輪的混合循環”發動機,韋斯解釋說,HAWC的助推器是一次性使用的。但甚至是DARPA都還沒有制定 研製 新型發動機的計畫,洛克希德仍然需要繼續完善這種推進技術。這樣的一架飛機的造價可以低於10億美元,休森說。“最重要的是,我們正在證明...
第四循環:感覺信息的定製化,或者稱為服務信息的定製化,使不斷購買的老客戶得到不同的服務感受。上面各個循環中,各類定製化處理後,與企業發生交易的客戶占客戶群的比例是逐漸增大的。模型運行中有幾個關鍵:定製化的前提是處理的客戶群達到一定規模,否則不僅沒有行銷方面的意義,而且會增大運行成本,達到什麼程度時...
心室顫動的波形、振幅與頻率均極不規則,無法辨認P波、QRS波群、ST段與T波,頻率達150~300次/分。治療 一般來說,VF治療選擇包括三類,分別是藥物治療、植入型心律轉復除顫器(ICD)和射頻導管消融觸發病灶。室顫發生後應立即進行搶救,力爭在數分鐘內建立有效的呼吸和循環,否則將發生腦細胞的不可逆性損傷,最終...
