基本介紹
- 中文名:撓率形式
- 外文名:torsion forms
- 領域:數學
- 定義:刻畫聯絡對稱性的二次形式
- 空間:仿射聯絡空間
- 對象:局部余標架場
概念


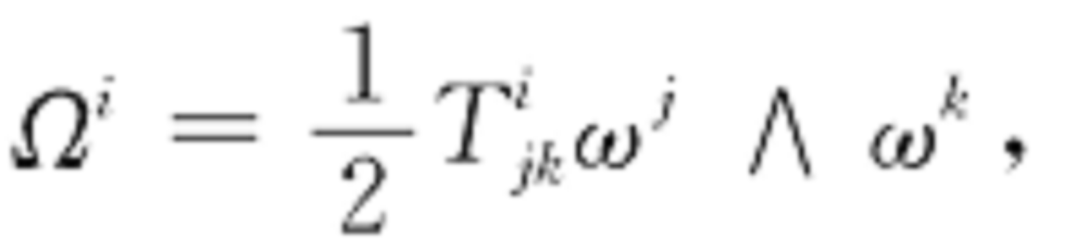
仿射聯絡
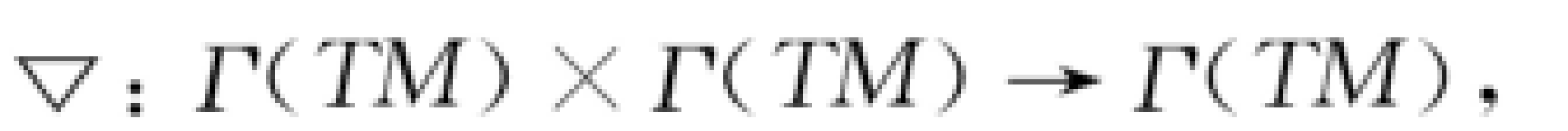

















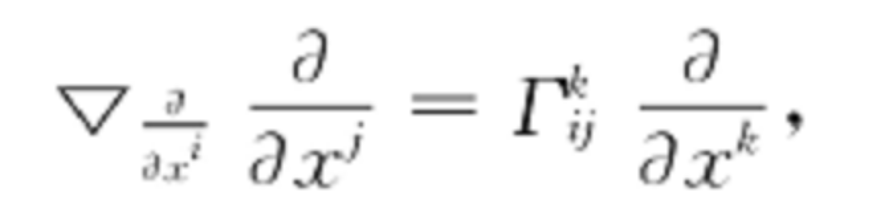
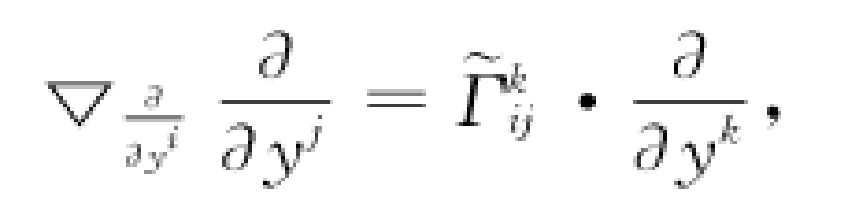
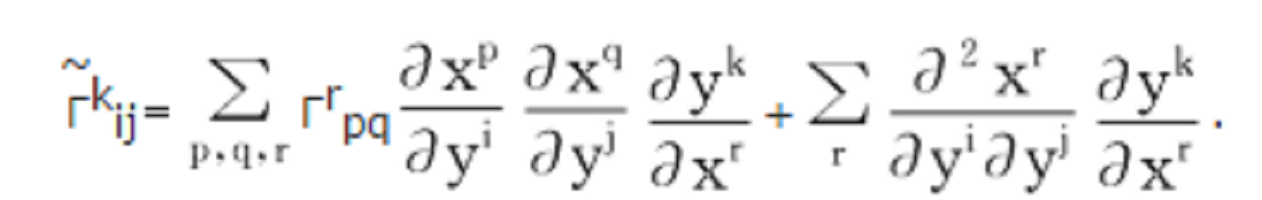




么正標架場
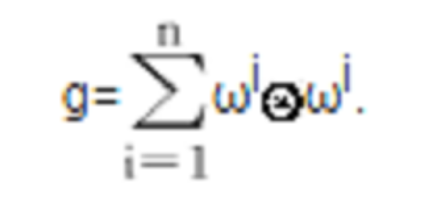


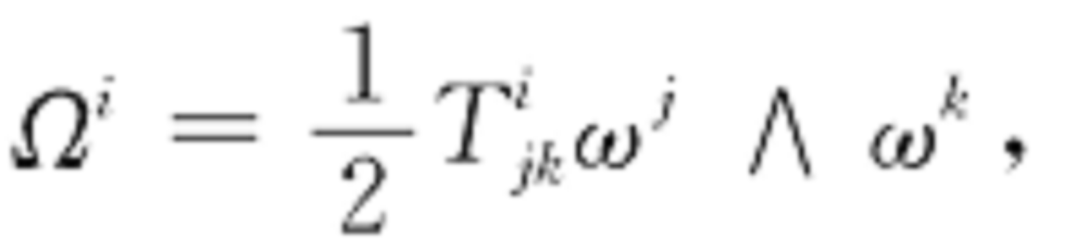
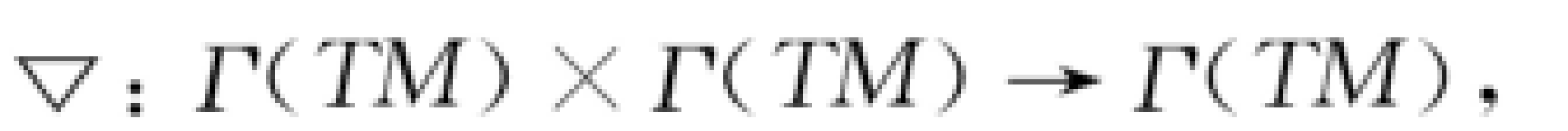

















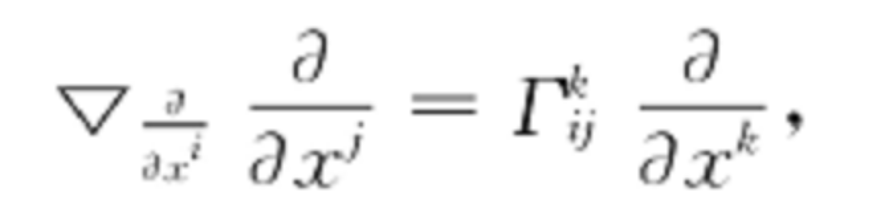
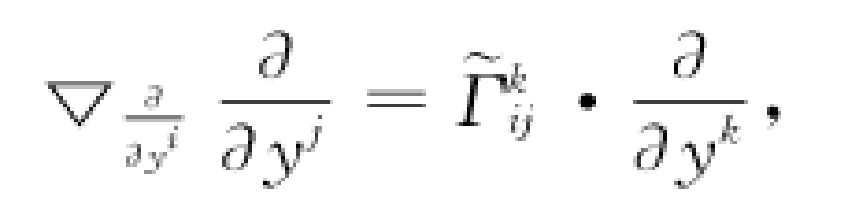
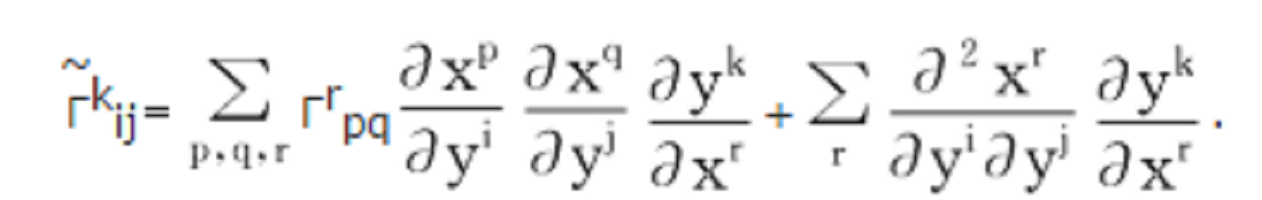




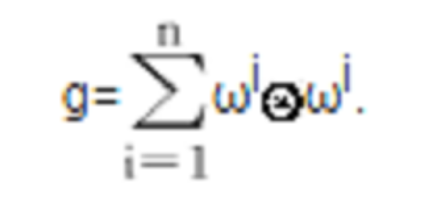
撓率形式(torsion forms)是刻畫聯絡對稱性的二次形式。仿射聯絡簡稱聯絡。主叢上的一種微分幾何結構。所謂仿射聯絡應該是以仿射變換群為結構群的主叢上的聯絡,在以一般線性群為結構群的主叢上的聯絡稱為線性聯絡。概念撓...
與其對應的是代數拓撲中的“Reidemeister撓率”,著名的Cheeger-Müller定理指出這兩個不變數是等價的。1995年,Bismut-Lott推廣“Ray-Singer解析撓率”到纖維叢的情形得到了“Bismut-Lott實解析撓率形式”。申請人與其合作者將運用運算元的散射...
《解析撓率的研究》是依託南開大學,由蘇廣想擔任項目負責人的青年科學基金項目。中文摘要 解析撓率是整體微分幾何的一個重要研究內容。解析撓率是由Ray和Singer於1971年左右通過緊流形上的拉普拉斯運算元定義的。Carely, Lott,Mathai等後來定義...
如果 是標架叢上的典範向量值1形式,聯絡形式 ω 的撓率是由結構方程定義的向量值2形式:這裡D代表外共變導數。第一比安基恆等式(對於標架叢的有撓率聯絡)取以下形式:第二比安基恆等式對於一般有聯絡的叢成立,並有如下形式:
撓率形式,是撓率的另一種刻畫,適用於M的標架叢FM。這個主叢裝備有一個聯絡形式ω,一個gl(n)-值的 1-形式將豎直矢量映到gl(n) 中的右作用的生成元,且通過在gl(n) 上的伴隨表示等變糾纏於 GL(n) 在 FM的切叢上的右作用...
用於描述一條曲線在一點偏離密切平面的程度。為了描述這種偏離度,我們將用到密切平面的變化率,也就是密切平面的法向量 的變化率,這樣就導出曲線的“撓率”這一概念。定義 稱為曲線在點 處的撓率。顯然平面曲線的撓率恆為零。
一個聯絡形式的主要張量性不變數是其曲率形式。如果有將向量叢與切叢等價的一個焊接形式,則有另一個不變數:撓率形式。在許多情形,考慮有附加結構的向量叢上的聯絡形式:即帶有結構群的纖維叢。
5.4.2 撓率張量和撓率形式 143 5.4.3 列維-齊維塔聯絡 145 5.4.4 協變微分 147 附錄5.4 列維-齊維塔生平及學術貢獻 150 5.5 黎曼曲率和結構方程 151 5.5.1 平行移動和測地線 151 5.5.2 仿射聯絡的...
在微分幾何中,黎曼曲率張量或黎曼曲率是表達黎曼流形的曲率的標準方式,更普遍的,它可以表示有仿射聯絡的流形的曲率,包括無撓率或有撓率的。簡介 曲率張量通過列維-奇維塔聯絡(更一般的,一個仿射聯絡)(或者叫協變導數)由下式給出:...
形式化定義 設 為一黎曼流形(或偽黎曼流形),則仿射聯絡 在滿足以下條件時是列維-奇維塔聯絡。無撓率:也就是,對任何向量場 我們有 ,其中 是向量場 和 的李括弧。與度量相容:也就是,對任何向量場 我們有 ,其中...
這裡,作為作為 1-形式矩陣 ω ∈ Ω(M)⊗gl(n)。一個容許聯絡是 ω 在G的李代數g上的一個取值。G-結構的撓率 任何G-結構伴隨有撓率,和聯絡的撓率有關。注意到一個給定的G-結構可能有許多不同的容許聯絡,這些聯絡可能有...
3.2 曲面的第一和第二基本形式 3.3 曲面上的曲線 法曲率 測地曲率和測地撓率 3.4 曲面的主曲率 歐拉公式 高斯曲率和平均曲率 3.5 曲面上向量的平行移動 3.6 閉曲面的高斯波涅公式 第四章 整體微分幾何初步 ...
殆復結構的撓率張量 在每一點 是餘切空間 的一個基,二次外形式 其中 上式又可寫成 其中 ()是一個以矢量為值的 次形式,我們稱它為殆復結構的撓率張量。當殆復結構的撓率為0,便說殆復結構是可積的。定理1:在一個實解析的...
殆復結構的撓率張量 在每一點 是餘切空間 的一個基,二次外形式 其中 上式又可寫成 其中 ()是一個以矢量為值的 次形式,我們稱它為殆復結構的撓率張量。當殆復結構的撓率為0,便說殆復結構是可積的。定理1:在一個實解析的...
