基本介紹
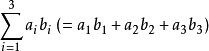
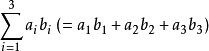
在數學裡,特別是將線性代數套用到物理時,愛因斯坦求和約定(Einstein summation convention)是一種標記的約定,又稱為愛因斯坦標記法(Einstein notation),在處理關於坐標...
愛因斯坦求和約定這本書以後如無相反的說明,相同的英文指標總表示從1至3求和。...... 愛因斯坦求和約定這本書以後如無相反的說明,相同的英文指標總表示從1至3求和...
其中,注意,之後的方程如果使用愛因斯坦求和約定,不會特別註明。已經知道里奇張量 ,現在就可以用里奇張量來定義里奇曲率。如果 為 點的單位向量,則...
而一樣的,上面使用了愛因斯坦求和約定。包立矩陣和內積、外積的關係 將泡利矩陣的對易和反對易相加得:因此可得:將它轉換成向量積的表達式:...
其中,注意,之後的方程如果使用愛因斯坦求和約定,不會特別註明。已經知道里奇張量 ,如今就可以用里奇張量來定義里奇曲率。如果 為 點的單位向量,則...
用愛因斯坦求和約定,上式右方在局部座標中可表示為:當M是緊緻時,則φ稱為調和映射,若φ是能量泛函E的一個臨界點。這個定義可以延伸至M不是緊緻的情況:φ稱為...
而一樣的,上面使用了愛因斯坦求和約定。泡利矩陣內積外積關係 將泡利矩陣的對易和反對易相加得:因此可得:為了避免符號重複,將a,b,c改成p,q,r,然後把上式和...
矢量分析中,在表達式的某一單項式之中出現且僅出現2次的下標,稱為啞指標。對這種指標應當進行遍歷求和。矢量和張量分析中,啞指標和愛因斯坦求和約定聯繫在一起。...
這裡Aa是四維勢,逗號表示對角標做偏導數並使用了愛因斯坦求和約定。這個規範的好處是具有洛侖茲不變性。洛侖茲規範\partial_{a}A^a ...
為 上的任意向量(假設有愛因斯坦求和約定),且有 是線性運算元。則有所以有 是運算元 在固定基底下的矩陣表示。 不依賴於 的選取,且有 若且唯若 。因此在固定基底...
A.2 張量的表示法及愛因斯坦求和約定A.3 克羅內克符號和置換符號A.4 對稱張量與反對稱張量A.5 二階張量的代數運算A.6 張量的微分和積分運算附錄B 格子張量...
將的下標拉高為上標,可以得到反變張量。採用愛因斯坦求和約定,這程式表達為給予一個階反對稱共變張量,則其階對偶張量(dual tensor)是一個反對稱反變張量:...
採用愛因斯坦求和約定,由於 ,給定方向餘弦矩陣A ,則可設定附體參考系B的取向,也就是剛體的取向。反過來,經過一番運算,可以得到 。給定位置向量 ...
採用愛因斯坦求和約定,則四維矢量的協變坐標和反變坐標之間的關係為。閔可夫斯基度規與它的“共軛度規張量” 相等:。四維矢量動力學 編輯 ...
使用愛因斯坦求和約定寫成:。 共變和反變反變分量 編輯 在歐幾里得空間裡,共變向量和反變向量之間的區分很小。這是因為能夠使用內積運算從向量求得余向量;對於所有...
其中下標代表費米子代,根據愛因斯坦求和約定,各項中重複的下標會把三代的結果都加起來,而、和分別代表夸克的左手性雙重態、右手性上單重態和右手性下單重態,和則...
這裡(下面同樣如此)使用了愛因斯坦求和約定,所以上式其實是一個關於i的和式。一個數量函式f的梯度利用流形上內積可定義為對位於流形在x點的切空間中所有向量 ...
這種表示縮並的方式與愛因斯坦求和約定類似,但此表示法只是抽象的記號而已,並不表示求和運算。抽象指標記號特徵 編輯 與不帶指標的字母(如T)表示張量相比,抽象指標...
質量殼方程經常用四維動量來表達,並使用愛因斯坦求和約定和c= 1的單位制,也就是 或者 。費曼圖中和內部傳播子相關的虛擬粒子通常允許離殼,但該進程的幅度通常隨著...
這裡A 是四維勢, 逗號表示對角標做偏導數並使用了愛因斯坦求和約定。這個規範的好處是具有洛倫茲不變性。在一般的矢量寫法並採用國際單位制下:...
是八個實數,並使用愛因斯坦求和約定。蓋爾曼矩陣的平方和給出了二次卡西米爾運算元蓋爾曼矩陣套用 編輯 蓋爾曼矩陣在強子分類中有重大意義。 為u,d夸克SU(2)同位旋空間...
這裡使用了愛因斯坦求和約定。以上同構稱為降號音樂同構(flat)用符號 表示,例如以上的函式 可表示成: ;而其逆運算稱為升號(sharp)用符號 表示:降號下降指標,升...
上式使用了愛因斯坦求和約定,其中γ為狄拉克矩陣。 [1] 費曼斜線標記恆等式 編輯 透過使用狄拉克矩陣的反對易關係,可以證明任何 與 滿足...
作者提出了一套新的符號系統和運算法則用於矢量和張量的運算,取代傳統的上下指標表示和愛因斯坦求和約定的方法。其主要特點是把坐標系作為一種特別的數學變數,給出其...
質量殼方程經常用四維動量來表達,並使用愛因斯坦求和約定和c= 1的單位制,也就是 或者 。費曼圖中和內部傳播子相關的虛擬粒子通常允許離殼,但該進程的幅度通常隨著...
